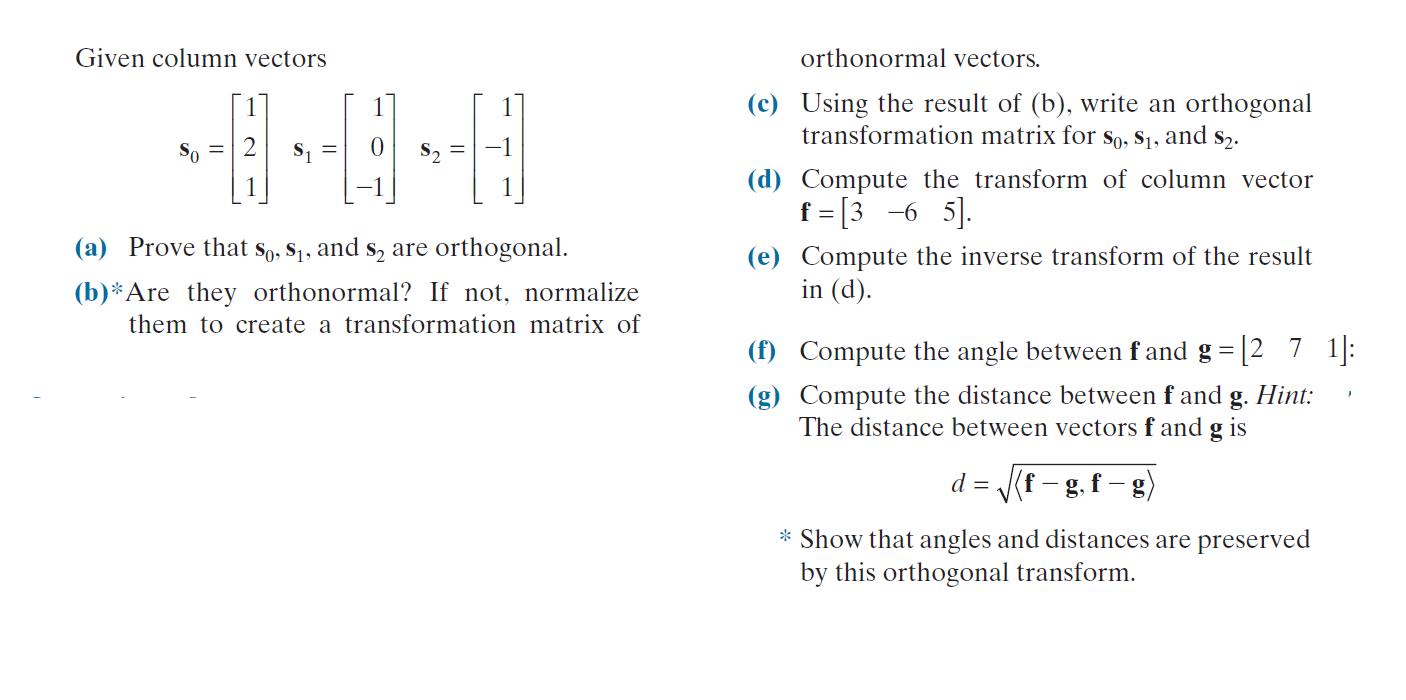
Given column vectors --4-4 (a) Prove that So, $, and $ are orthogonal. (b)*Are they orthonormal? If not, normalize them to create a transformation matrix of orthonormal vectors. (c) Using the result of (b), write an orthogonal transformation matrix for So, $1, and $. (d) Compute the transform of column vector f = [3 -6 5]. (e) Compute the inverse transform of the result in (d). (f) Compute the angle between fand g=[2_7_1]: (g) Compute the distance between f and g. Hint: The distance between vectors f and g is d = (f-g, f-g) * Show that angles and distances are preserved by this orthogonal transform.