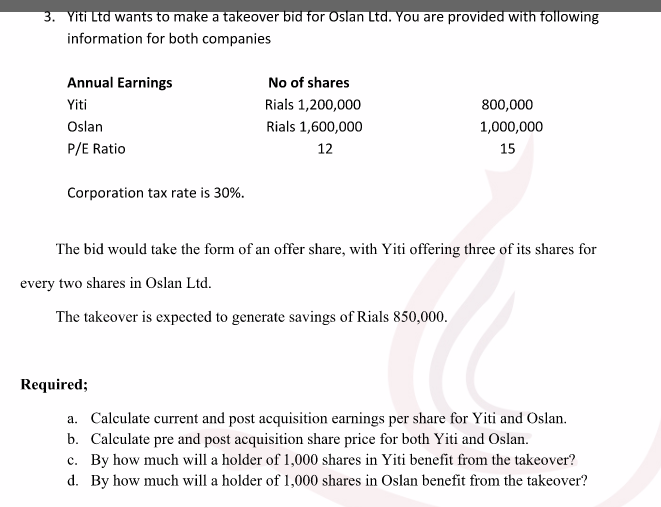
If the function f(t) is a solution of the initial _value problem y' = (t + 2)y, y(0) = 3, find f(0) and f'(0). Show that the function f(t) = 3/2 e^t^2 - 1/2 is a solution of the differential equation y' - 2ty = t. Show that the function f(t) = t^2 - 1/2 is a solution of the differential equation (y')^2 - 4y = 2. Show that the function f(t) = 5e^2t satisfies y"-3y' + 2y = 0, y(0) = 5, y'(0) = 10