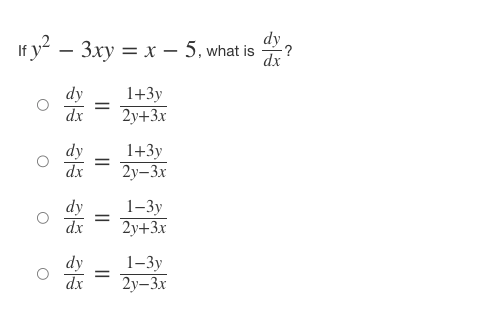
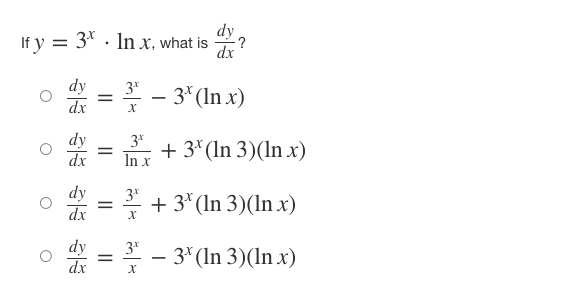
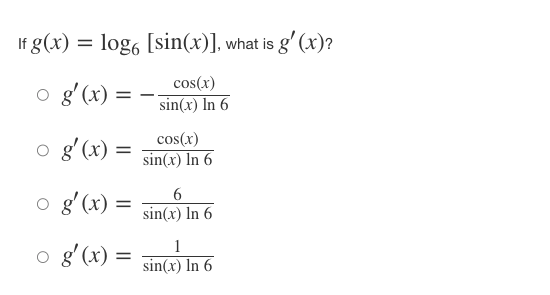
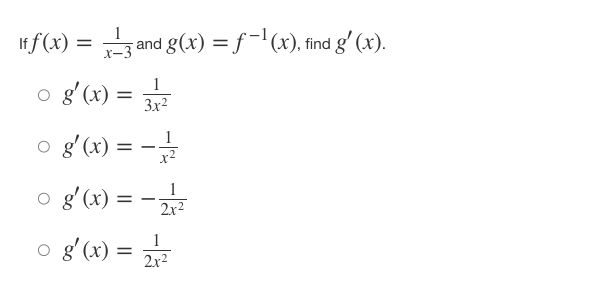
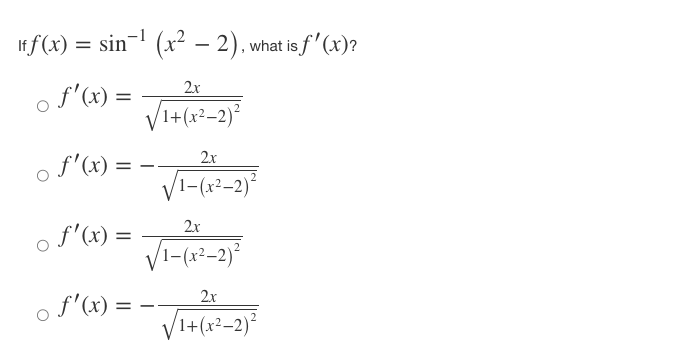
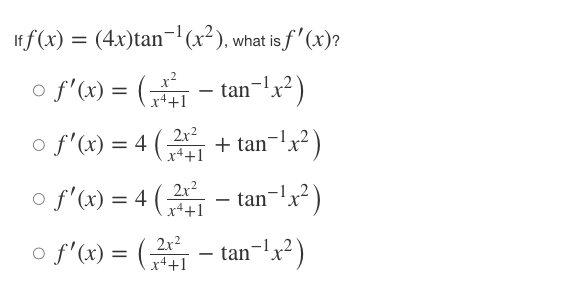
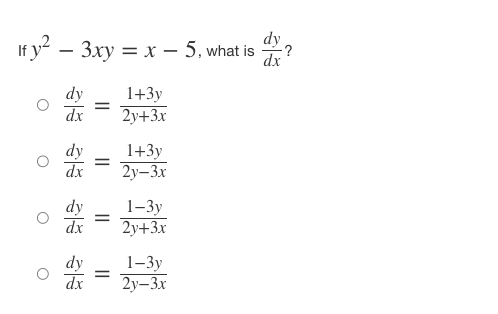
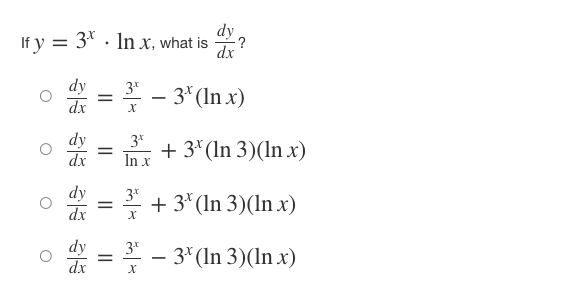
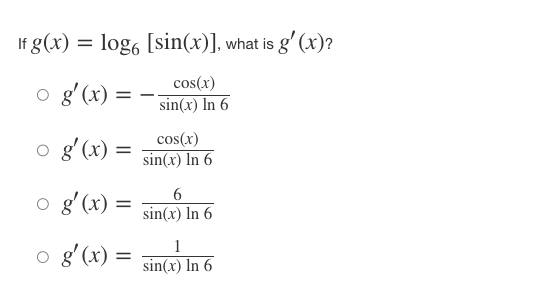
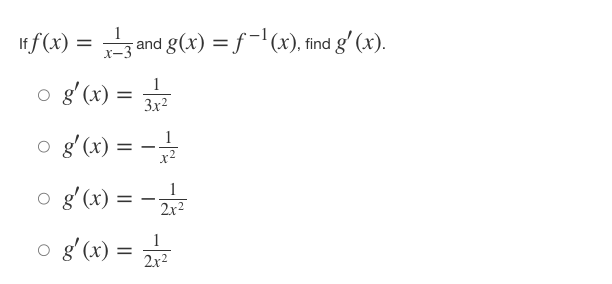
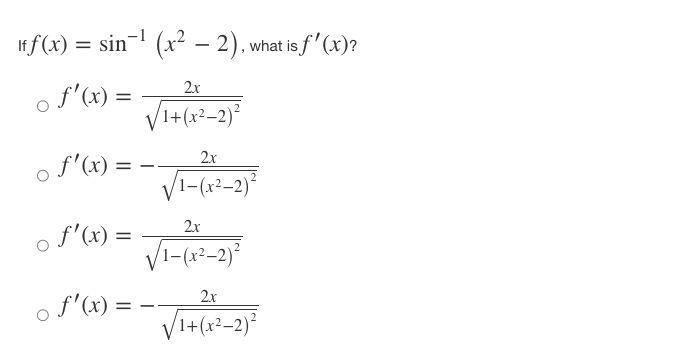
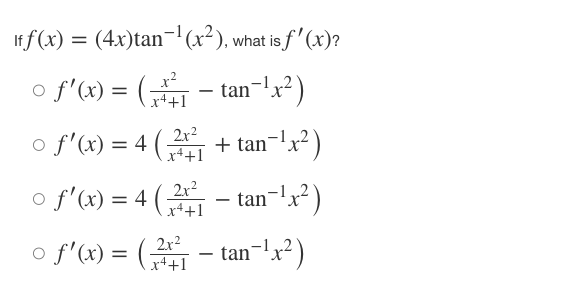
Iff ( x ) = x' + - and 8(x) = f-(x), find the slope of the curve g(x) = f- (x) at the point (2, 1). 0 8' (2) = -7 o g' (2) = 1 o g' (2) = o g' (2) = N/ - Iff(x) = (4x)tan-(x-), what isf (x)? of' ( x ) = ( *4+1 - tan x2 of' ( x ) = 4 2x2 r4+1 + tan -1,2 of' (x ) = 4 2x2 - tan 1 2 x4+1 of' ( x ) = ( 2x2 x4+1 - tan