Question: Ify=f(x) write f(x)in Leibniz notation. Ify= y=y(x), writeyin Leibniz notation. fIf f(x) = e2* [sin(x)]', what is f'(x)? O f'(x) - 2e2 [ sin(x) ]2

$Ify=f(x) write f(x)in Leibniz notation.Ify= y=y(x), writeyin Leibniz notation. \fIf f(x)$

]2 - 2e2* cos(are ) sin(a) O f'(x) = ex [sin(x)]2 -

2e2 [cos(2x)] O f'(::) = 2-27 [sin (::)]' + 2e2 cos(:) sin(a:)

$o S'(x) = e2. [sin(x)]2 + 2e27 [cos(2x)]\fIf f(x) = (4x)tan-1(x2 ),$

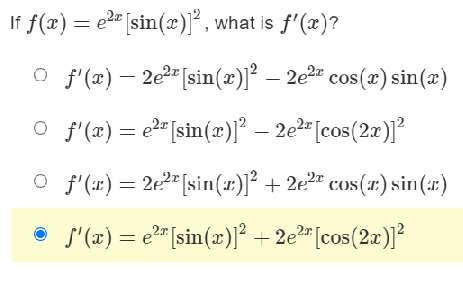
what is f'(x)? of'(x) = 41 cty +tan 1,2 of'(x) = -

tan 1 of'(x) -4 - tan z? of'(:) = - t.an 1

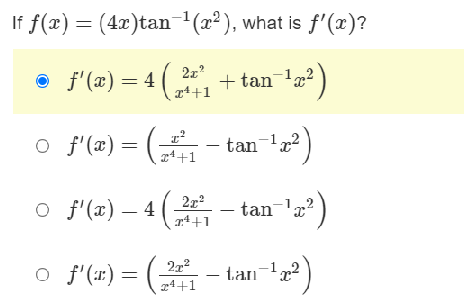
Ify=f(x) write f(x)in Leibniz notation.

Ify= y=y(x), writeyin Leibniz notation.

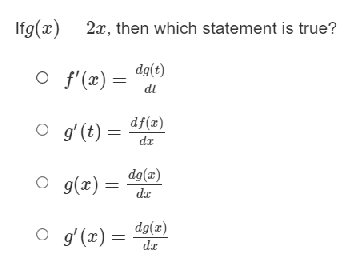
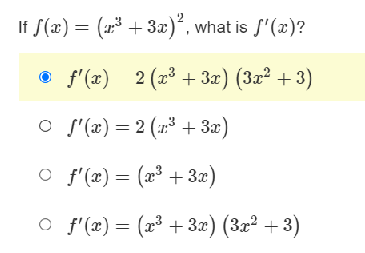
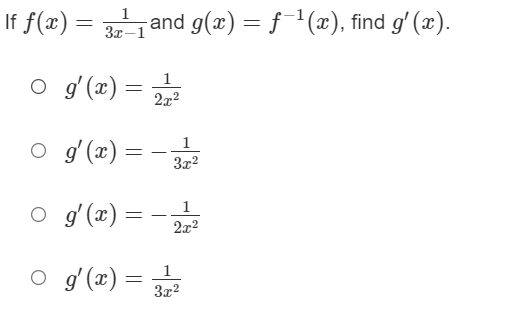
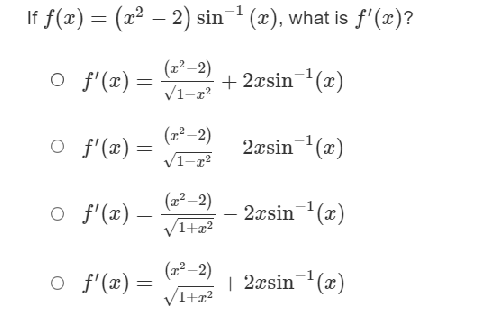
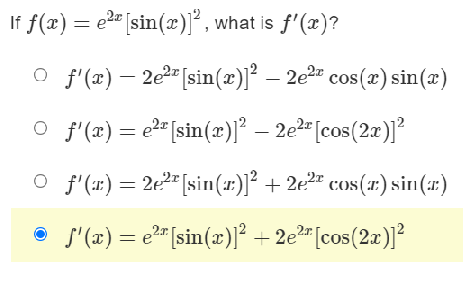
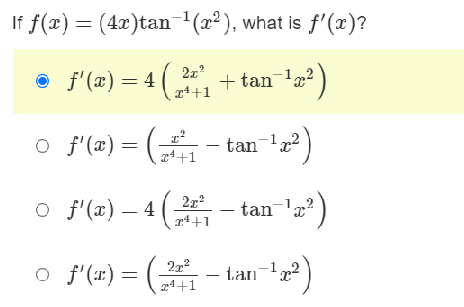
\fIf f(x) = e2* [sin(x)]', what is f'(x)? O f'(x) - 2e2 [ sin(x) ]2 - 2e2* cos(are ) sin(a) O f'(x) = ex [sin(x)]2 - 2e2 [cos(2x)] O f'(::) = 2-27 [sin (::)]' + 2e2 cos(:) sin(a:) o S'(x) = e2. [sin(x)]2 + 2e27 [cos(2x)]\fIf f(x) = (4x)tan-1(x2 ), what is f'(x)? of'(x) = 41 cty +tan 1,2 of'(x) = - tan 1 of'(x) -4 - tan z? of'(:) = - t.an 1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Iff (X) = sin(X) COS(X), what is f ' (X)? o f'(X) = cos(x) sin(x) O f '(X) = (30800 + sin(x) O f '(X) = cos(x) + sin(x) O f '(X) = COS(X) sin(X) If y = f(X), write f "(X) in Leibniz notation. Enter...

gray (tmg2549) - HW14 - hamrick - (53665) This print-out should have 23 questions. Multiple-choice questions may continue on the next column or page - find all choices before answering. 001 5. f (x)...

4 / 11 / 22 1Estefania Hagins Math 200 Problem 8. A baseball is launched into the air with an upward velocity of 106 feet per second. The height of the baseball after t seconds can be represented by...

Exercise Set 5.3: Graphs of the Tangent, Cotangent, Secant, and Cosecant Functions (f) Give an interval, if one exists, on which f ( x ) = tan ( x ) is increasing. Then give an Answer the following....

MATH 115 Precalculus Fall, 2016, V1.1 MATH 115 FINAL EXAMINATION This is an open-book exam. You may refer to your text and other course materials as you work on the exam, and you may use a...

buckley (jdb4687) - HW06 - beshaj - (53521) This print-out should have 32 questions. Multiple-choice questions may continue on the next column or page - find all choices before answering. 001 003 2...

I. What I Know (Pre-Test) Instruction: Choose the letter of the correct answer to the following items. Write them on a separate sheet of paper. 1. If y = f(g(x)) where y = ese'x, choose f(x) such...

Need solutions 1. If f(x) = sin (x), find f a. 0 C. b. 1 d. 2. If f(x) = Sin X find f * COS X a. 1 C. b. -2 d. 2 3. Find the slope of the tangent to the curve y = 2 sin'x at x = a. C. -1 b. 3 d. 4....

Ohio Household Products Co. (OHPC) is a diversified household-cleaner processing company. The companys Mishawaka plant produces two products: an appliance cleaner and a general-purpose cleaner from a...

Two resistances R=X. ohms and R=1 ohms are connected to a wire AB of uniform resistivity, as shown in the figure. The radius of the wire varies linearly along its axis from 0.2mm at A to 1mm at B. A...

1 2 . d . Why would a fixed - charge coverage ratio be materially different from an interest coverage ratio?

what the 2 min video and answer the questions https://youtu.be/MXo_d6tNWuY 1. This Video first aired in 2015. Has this occurred? Why/why not? Justify your answer. 2. What consumer value is being...

6. How can a message directly influence the interpreter?

1. Discuss the following statements: (a) The dangers of mountain driving in an old Lada 4 4, and safety concerns. (b) We perceive the world backwards. (c) Numbers are different from words, but they...

5. How can a sender (utterer) directly influence the interpreter (receiver)?