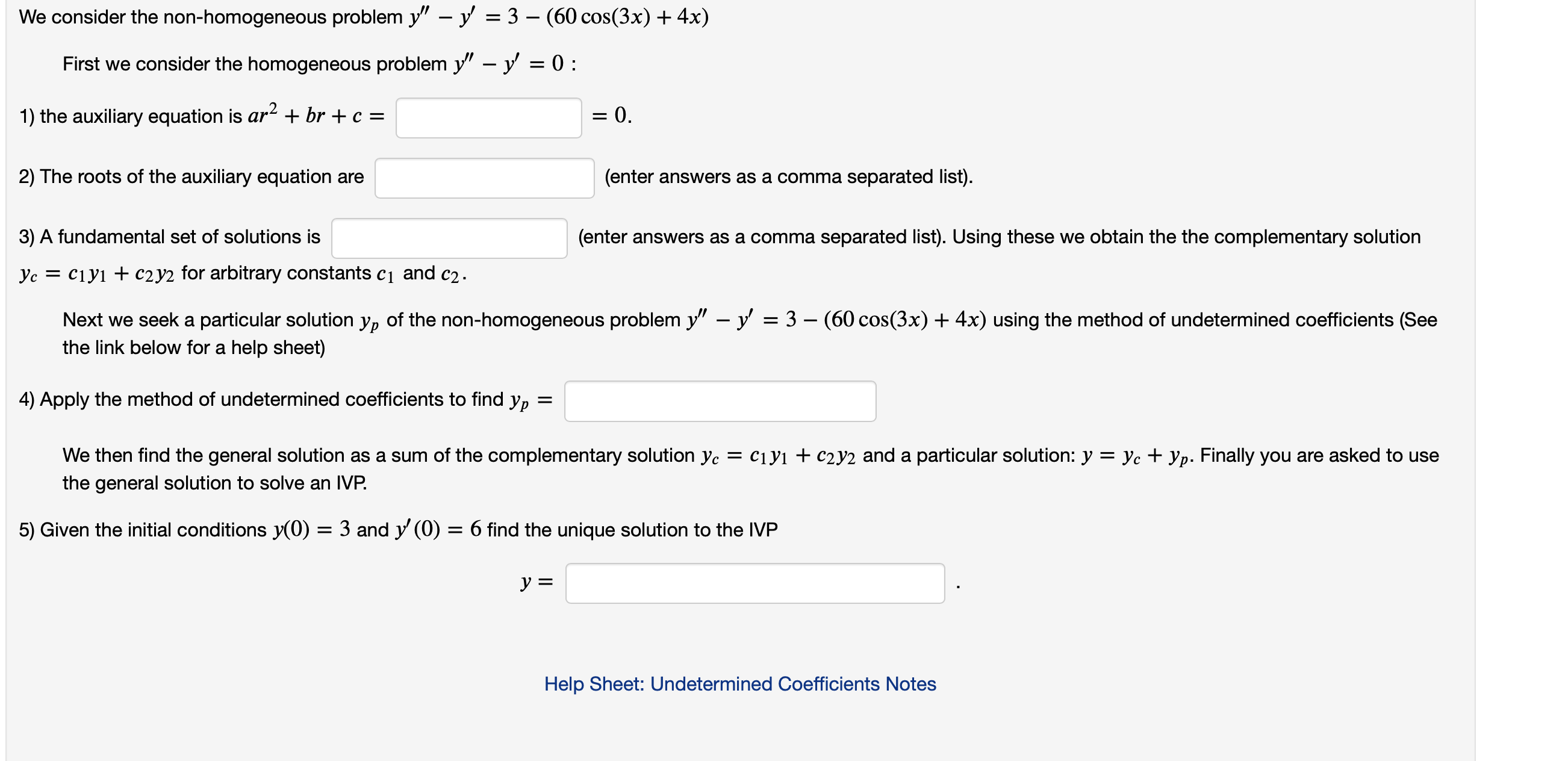
Question: I'll attach two questions below Will rate if helpful! thanks (1 point) We consider the non-homogeneous problem y y' = 60 cos(3x) First we consider
I'll attach two questions below Will rate if helpful! thanks

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


