Implement a function, solve_neq(X, y) that implements Algorithm 1. It should return a Numpy vector containing the model parameter estimates.

Steps of the algorithm:

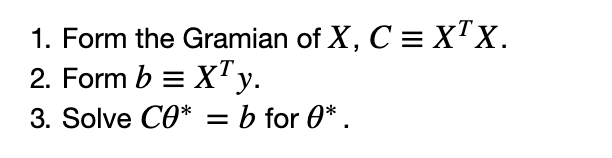
Your algorithm should carry out these steps. For the third step, use Scipy's routine, scipy.linalg.solve(). It has an option that allows you to indicate that C is symmetric and positive definite, which will be true of C for our synthetic problem.

The code cell will run your function to compute a set of parameter estimates. It will store these in a variable named theta_neq.

1. Form the Gramian of X, CXTX 3. Solve C0"-b for * . print(x.T.dot(x)) print (X.T.dot(y)) def solve _neq(X, y): ## YOUR CODE HERE theta-neq solve-neg(x, y) = print("Your implementation's show-2vecs-tibble ( theta-neg , solution versus the true solution:") theta-true , xname='theta-neg ', yname='theta-true', error=True ) # Test cell: solve-neg-test try: del np.linalg.lstsq solve_neq(X, y) if re.findall('lstsq, n.args[0]): raise n if re.findall('1stsq, a.args[o]): raise a np.1inalg.lstsq = SAVE LSTSQ except NameError as n: print(***Double-check that you did not try to use lstsq).*** except AttributeError as a: print("*** Double-check that you did not try to use lstsg)'.*** finally: assert type(theta neq) is np.ndarray, "theta_neq should be a Numpy array, but isn't." assert theta_neq. shape (n+l, 1)theta_neq. shape is instead of (>.".format (theta_neq. shape, (n+1, 1) assert (np.abs (theta neq - theta true)