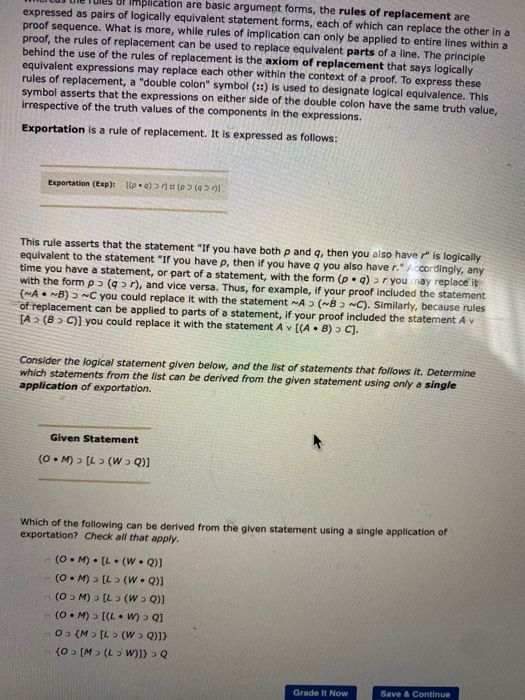
Question: Implication are basic argument forms, the rules of replacement are expressed as pairs of logically equivalent statement forms, each of which can replace the other
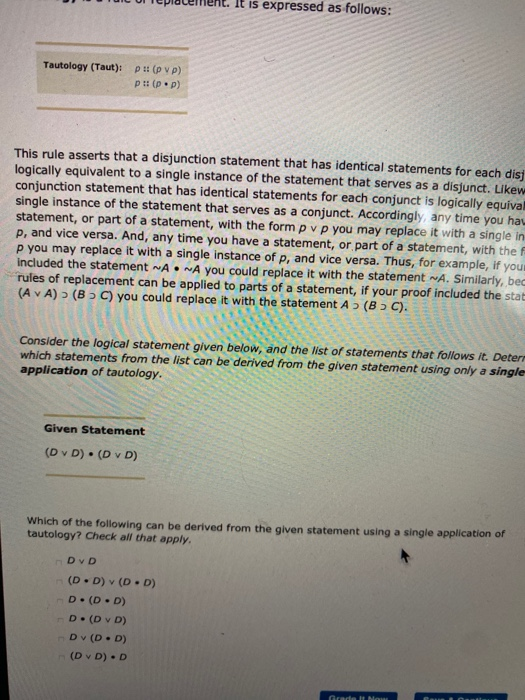
Implication are basic argument forms, the rules of replacement are expressed as pairs of logically equivalent statement forms, each of which can replace the other in a proof sequence. What is more, while rules of Implication can only be applied to entire lines within a proof, the rules of replacement can be used to replace equivalent parts of a line. The principle behind the use of the rules of replacement is the axiom of replacement that says logically equivalent expressions may replace each other within the context of a proof. To express these rules of replacement, a "double colon" symbol (::) is used to designate logical equivalence. This symbol asserts that the expressions on either side of the double colon have the same truth value, irrespective of the truth values of the components in the expressions. Exportation is a rule of replacement. It is expressed as follows: Exportation (Exp): 6.0) ( This rule asserts that the statement "If you have both p and q, then you also have r" is logically equivalent to the statement "If you have p, then if you have a you also have r. Accordingly, any time you have a statement, or part of a statement, with the form (p.a) or you may replace it with the form po (gr), and vice versa. Thus, for example, if your proof included the statement (NAB) > C you could replace it with the statement A (BC). Similarly, because rules of replacement can be applied to parts of a statement, if your proof included the statement A v [A2 (8) C)] you could replace it with the statement Av [(AB) C). Consider the logical statement given below, and the list of statements that follows it. Determine which statements from the list can be derived from the given statement using only a single application of exportation. Given Statement ( OM) [2(W)] Which of the following can be derived from the given statement using a single application of exportation? Check all that apply. (0.M). [L. (W.Q)] (OM) - [L (W.Q)] (OM) - [L (W 0) (OM) [( LW) Q1 0 (M) [L ( WQ)]) (O [M ( LW) Q Grade It Now Save & Continue It is expressed as follows: Tautology (Taut): P!! (pvp) p(p.) This rule asserts that a disjunction statement that has identical statements for each disj logically equivalent to a single instance of the statement that serves as a disjunct. Likew conjunction statement that has identical statements for each conjunct is logically equival single instance of the statement that serves as a conjunct. Accordingly any time you haw statement, or part of a statement, with the form pvp you may replace it with a single in p, and vice versa. And, any time you have a statement, or part of a statement, with the F p you may replace it with a single instance of p, and vice versa. Thus, for example, if you included the statement ~AA you could replace it with the statement ~A. Similarly, bec rules of replacement can be applied to parts of a statement, if your proof included the stat (A v A) (BC) you could replace it with the statement A (BC). Consider the logical statement given below, and the list of statements that follows it. Deter which statements from the list can be derived from the given statement using only a single application of tautology. Given Statement (DVD) (DVD) Which of the following can be derived from the given statement using a single application of tautology? Check all that apply. DVD (D.D) (D.D) D. (D.D) D. (DVD) DVD. D) (DVD).D Grace Mau Implication are basic argument forms, the rules of replacement are expressed as pairs of logically equivalent statement forms, each of which can replace the other in a proof sequence. What is more, while rules of Implication can only be applied to entire lines within a proof, the rules of replacement can be used to replace equivalent parts of a line. The principle behind the use of the rules of replacement is the axiom of replacement that says logically equivalent expressions may replace each other within the context of a proof. To express these rules of replacement, a "double colon" symbol (::) is used to designate logical equivalence. This symbol asserts that the expressions on either side of the double colon have the same truth value, irrespective of the truth values of the components in the expressions. Exportation is a rule of replacement. It is expressed as follows: Exportation (Exp): 6.0) ( This rule asserts that the statement "If you have both p and q, then you also have r" is logically equivalent to the statement "If you have p, then if you have a you also have r. Accordingly, any time you have a statement, or part of a statement, with the form (p.a) or you may replace it with the form po (gr), and vice versa. Thus, for example, if your proof included the statement (NAB) > C you could replace it with the statement A (BC). Similarly, because rules of replacement can be applied to parts of a statement, if your proof included the statement A v [A2 (8) C)] you could replace it with the statement Av [(AB) C). Consider the logical statement given below, and the list of statements that follows it. Determine which statements from the list can be derived from the given statement using only a single application of exportation. Given Statement ( OM) [2(W)] Which of the following can be derived from the given statement using a single application of exportation? Check all that apply. (0.M). [L. (W.Q)] (OM) - [L (W.Q)] (OM) - [L (W 0) (OM) [( LW) Q1 0 (M) [L ( WQ)]) (O [M ( LW) Q Grade It Now Save & Continue It is expressed as follows: Tautology (Taut): P!! (pvp) p(p.) This rule asserts that a disjunction statement that has identical statements for each disj logically equivalent to a single instance of the statement that serves as a disjunct. Likew conjunction statement that has identical statements for each conjunct is logically equival single instance of the statement that serves as a conjunct. Accordingly any time you haw statement, or part of a statement, with the form pvp you may replace it with a single in p, and vice versa. And, any time you have a statement, or part of a statement, with the F p you may replace it with a single instance of p, and vice versa. Thus, for example, if you included the statement ~AA you could replace it with the statement ~A. Similarly, bec rules of replacement can be applied to parts of a statement, if your proof included the stat (A v A) (BC) you could replace it with the statement A (BC). Consider the logical statement given below, and the list of statements that follows it. Deter which statements from the list can be derived from the given statement using only a single application of tautology. Given Statement (DVD) (DVD) Which of the following can be derived from the given statement using a single application of tautology? Check all that apply. DVD (D.D) (D.D) D. (D.D) D. (DVD) DVD. D) (DVD).D Grace Mau