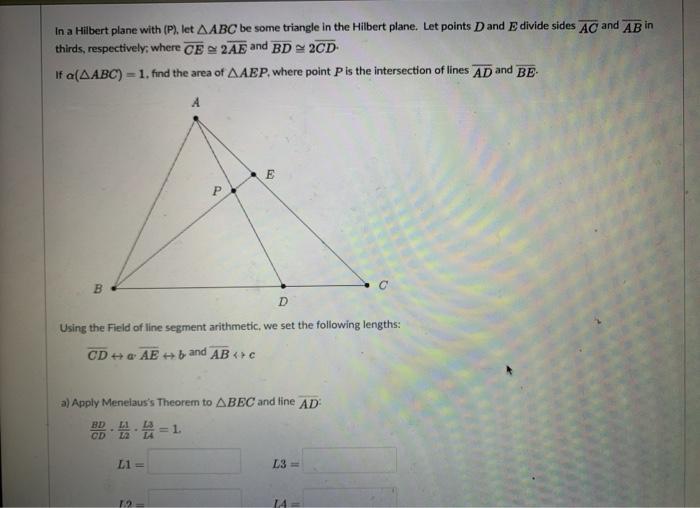
In a Hilbert plane with (P), let AABC be some triangle in the Hilbert plane. Let points Dand E divide sides AC and AR in thirds, respectively; where CE S 2AE and BD 2CD If a(AABC) =1, find the area of AAEP, where point Pis the intersection of lines AD and BE. A D Using the Field of line segment arithmetic, we set the following lengths: CD ++ a AE +b and AB +e a) Apply Menelaus's Theorem to ABEC and fine AD ,,=1 BD L1 = L3 = 14