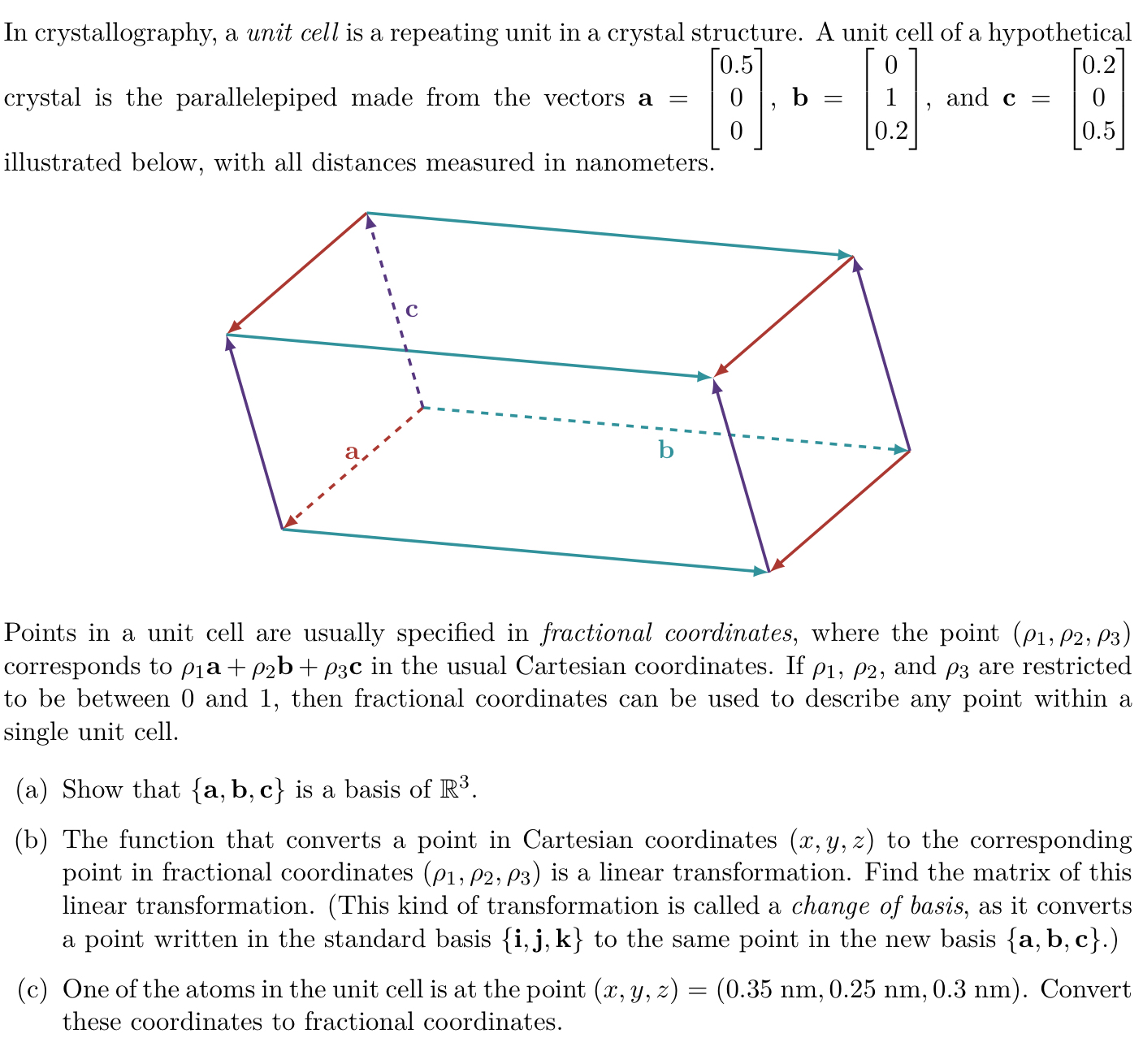
In crystallography, a unit cell is a repeating unit in a crystal structure. A unit cell of a hypothetical

crystal is the parallelepiped made from the vectors $a=\left[\begin{array}{c}0\mathrm{.}5\\ 0\\ 0\end{array}\right],b=\left[\begin{array}{c}0\\ 1\\ 0\mathrm{.}2\end{array}\right],$ and $c=\left[\begin{array}{c}0\mathrm{.}2\\ 0\\ 0\mathrm{.}5\end{array}\right]$

illustrated below, with all distances measured in nanometers.

Points in a unit cell are usually specified in fractional coordinates, where the point $({}_1,{}_2,{}_3)$

corresponds to ${}_{1}a+{}_{2}b+{}_{3}c$ in the usual Cartesian coordinates. If ${}_1,{}_2,$ and ${}_3$ are restricted

to be between $0$ and $1,$ then fractional coordinates can be used to describe any point within a

single unit cell.

$($a$)$ Show that $\{a,b,c\}$ is a basis of $R^3.$

$($b$)$ The function that converts a point in Cartesian coordinates $(x,y,z)$ to the corresponding

point in fractional coordinates $({}_1,{}_2,{}_3)$ is a linear transformation. Find the matrix of this

linear transformation. $($This kind of transformation is called a change of basis, as it converts

a point written in the standard basis $\{i,j,k\}$ to the same point in the new basis $\{a,b,c\}.)$

$($c$)$ One of the atoms in the unit cell is at the point $(x,y,z)=(0\mathrm{.}35nm,0\mathrm{.}25nm,0\mathrm{.}3nm).$ Convert

these coordinates to fractional coordinates.