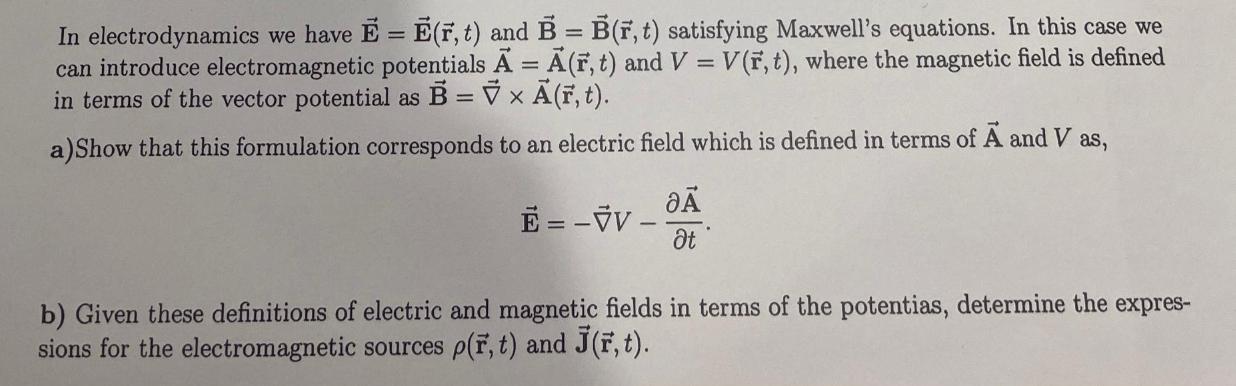
In electrodynamics we have E = E(r, t) and B = B(r, t) satisfying Maxwell's equations. In this case we can introduce electromagnetic potentials A= A(r, t) and V = V(r, t), where the magnetic field is defined in terms of the vector potential as B = V x A(r, t). a) Show that this formulation corresponds to an electric field which is defined in terms of A and V as, E-VV- O t b) Given these definitions of electric and magnetic fields in terms of the potentias, determine the expres- sions for the electromagnetic sources p(r, t) and J(F, t).