in matlab, please help with these quick functions

for reference

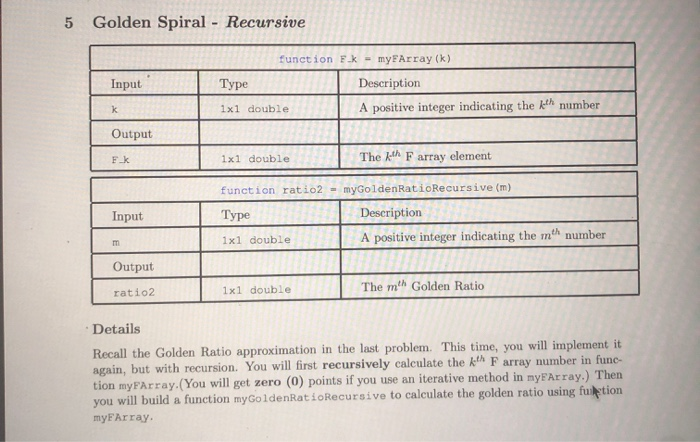
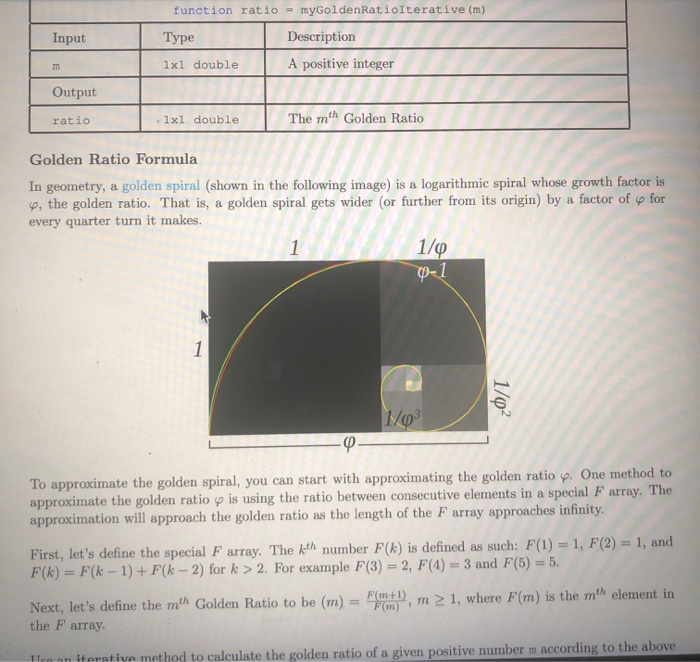
5 Golden Spiral - Recursive L function F.k - myFarray(k) Type Description 1x1 double A positive integer indicating the kth number Input k Output Fk 1x1 double The kth Farray element function ratio2 - myGoldenRatioRecursive (m) Type Description 1x1 double A positive integer indicating the mth number Input m l Output ratio2 1x1 double The m'h Golden Ratio Details Recall the Golden Ratio approximation in the last problem. This time, you will implement it again, but with recursion. You will first recursively calculate the fath F array number in func- tion my FArray (You will get zero (0) points if you use an iterative method in myFArray.) Then you will build a function my GoldenRatio Recursive to calculate the golden ratio using fuition myFArray function ratio = myGoldenRatioIterative (m) Type Description 1x1 double A positive integer Input m Output ratio | 1x1 double. The mth Golden Ratio Golden Ratio Formula In geometry, a golden spiral (shown in the following image) is a logarithmic spiral whose growth factor is 4, the golden ratio. That is, a golden spiral gets wider (or further from its origin) by a factor of y for every quarter turn it makes 1 1/8 0-1 1/02 103 00 To approximate the golden spiral, you can start with approximating the golden ratio yp. One method to approximate the golden ratio y is using the ratio between consecutive elements in a special F array. The approximation will approach the golden ratio as the length of the F array approaches infinity. First, let's define the special F array. The kth number F(k) is defined as such: F(1) = 1, F(2) = 1, and F(k) = F(k-1) + F(k - 2) for k > 2. For example F(3) = 2, F(4) = 3 and F(5) = 5. Next, let's define the meth Golden Ratio to be (m) = Pant!, m > 1, where F(m) is the m'h element in the F array. w anative method to calculate the golden ratio of a given positive number m according to the above