**In MATLAB**

Prove that the second degree Taylor Approximation... (see diagram for full question)

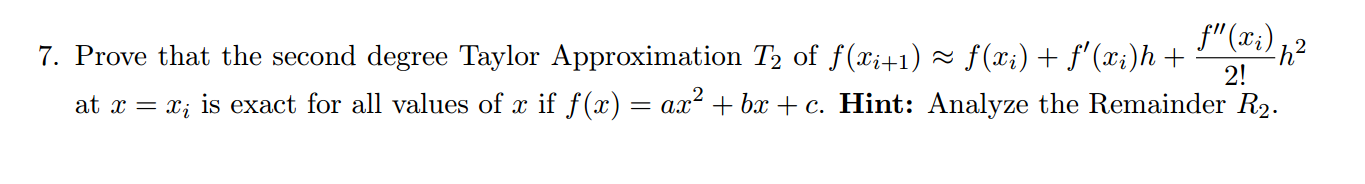
Prove that the second degree Taylor Approximation T_2 of f(x_i+1) ~ f(x_i) + f'(x_i)h + at x = Xi is exact for all values of x if f(x) = ax2 + bx + c. Analyze the Remainder R2. Prove that the second degree Taylor Approximation T_2 of f(x_i+1) ~ f(x_i) + f'(x_i)h + at x = Xi is exact for all values of x if f(x) = ax2 + bx + c. Analyze the Remainder R2