in ocaml language

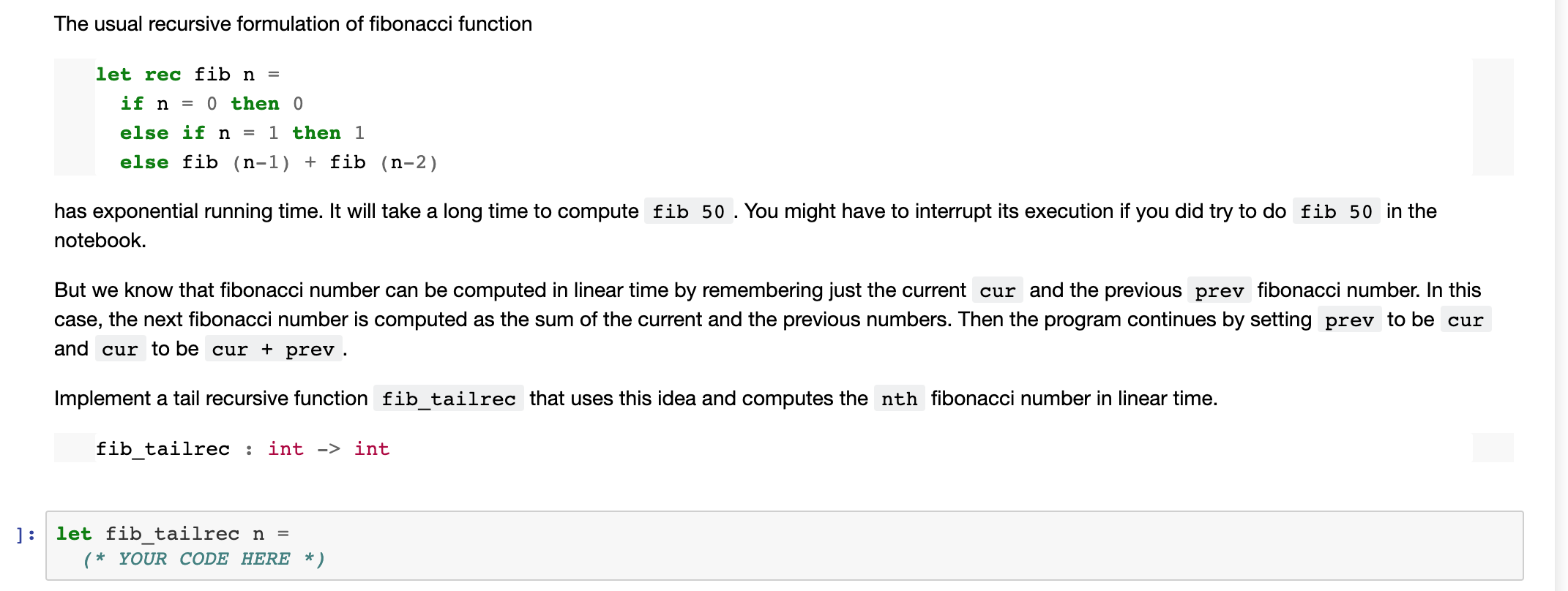
The usual recursive formulation of fibonacci function let rec fib n = if n = 0 then 0 else if n 1 then 1 else fib (n-1) + fib (n-2) has exponential running time. It will take a long time to compute fib 50 . You might have to interrupt its execution if you did try to do fib 50 in the notebook. But we know that fibonacci number can be computed in linear time by remembering just the current cur and the previous prev fibonacci number. In this case, the next fibonacci number is computed as the sum of the current and the previous numbers. Then the program continues by setting prev to be cur and cur to be cur + prev. Implement a tail recursive function fib_tailrec that uses this idea and computes the nth fibonacci number in linear time. fib tailrec : int -> int ] : let fib tailrec n (* YOUR CODE HERE *)