ocaml language

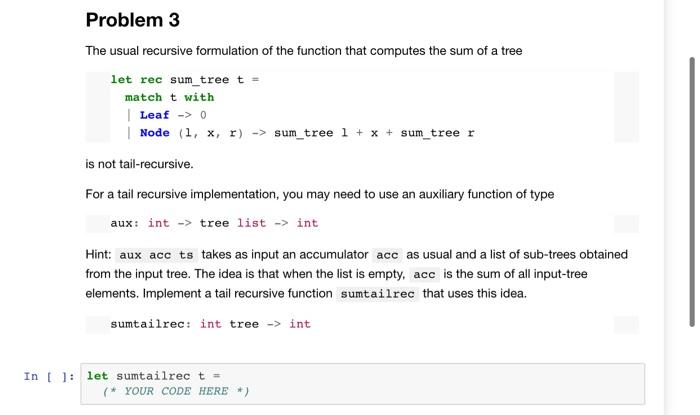
Library functions: You can use any library functions in the List module for this assignment (please do not use library functions in any other modules). You may find the following functions particularly useful, e.g., List.mapi, List.mem_assoc, and List.assoc. Datatypes: Problems 1-3 are about manipulating tree data structures. In OCaml, you can define a tree data structure using datatype: type 'a tree = Leaf Node of 'a tree * 'a * 'a tree We will assume binary search trees in this assignment and can define a bineary search tree insertion function as the following: let rec insert tree x match tree with Leaf -> Node (Leaf, x, Leaf) Node(1, y, r) -> if x = y then tree else if x insert acc x) Leaf 1 Problem 3 The usual recursive formulation of the function that computes the sum of a tree let rec sum_tree t = match t with Leaf -> 0 Node (1, x, r) -> sum_tree 1 + x + sum_treer is not tail-recursive. For a tail recursive implementation, you may need to use an auxiliary function of type aux: int -> tree list -> int Hint: aux acc ts takes as input an accumulator acc as usual and a list of sub-trees obtained from the input tree. The idea is that when the list is empty, acc is the sum of all input-tree elements. Implement a tail recursive function sumtailrec that uses this idea. sumtailrec: int tree -> int In [ ]: let sumtailrec t (* YOUR CODE HERE *) Library functions: You can use any library functions in the List module for this assignment (please do not use library functions in any other modules). You may find the following functions particularly useful, e.g., List.mapi, List.mem_assoc, and List.assoc. Datatypes: Problems 1-3 are about manipulating tree data structures. In OCaml, you can define a tree data structure using datatype: type 'a tree = Leaf Node of 'a tree * 'a * 'a tree We will assume binary search trees in this assignment and can define a bineary search tree insertion function as the following: let rec insert tree x match tree with Leaf -> Node (Leaf, x, Leaf) Node(1, y, r) -> if x = y then tree else if x insert acc x) Leaf 1 Problem 3 The usual recursive formulation of the function that computes the sum of a tree let rec sum_tree t = match t with Leaf -> 0 Node (1, x, r) -> sum_tree 1 + x + sum_treer is not tail-recursive. For a tail recursive implementation, you may need to use an auxiliary function of type aux: int -> tree list -> int Hint: aux acc ts takes as input an accumulator acc as usual and a list of sub-trees obtained from the input tree. The idea is that when the list is empty, acc is the sum of all input-tree elements. Implement a tail recursive function sumtailrec that uses this idea. sumtailrec: int tree -> int In [ ]: let sumtailrec t (* YOUR CODE HERE *)