Question: In P3, define Let W = span(po, P, P2) where po(t) = 1, p (t) = t, p(t) = t. a) Find an orthogonal

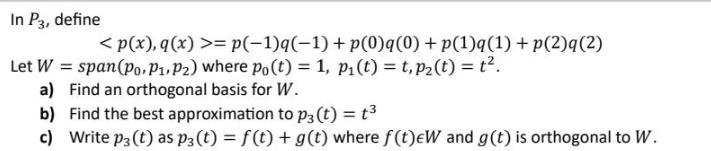
In P3, define Let W = span(po, P, P2) where po(t) =

In P3, define Let W = span(po, P, P2) where po(t) = 1, p (t) = t, p(t) = t. a) Find an orthogonal basis for W. = p(-1)q(-1) + p(0)q(0) + p(1)q(1) + p(2)q(2) b) Find the best approximation to p3 (t) = t c) Write p3 (t) as p3 (t) = f(t) + g(t) where f(t)EW and g(t) is orthogonal to W.

Step by Step Solution

★★★★★

3.40 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

In this problem were dealing with an inner product space defined by the inner product p1q1 p0q0 p1q1 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Supply Chain Linear Program Problem 1st discription sets up original problem. 2nd discription changes problem with direct sourcing from factories Thank you! Network Design Case Study You work for a...

Let V = P(4) denote the space of quartic polynomials, with the L2 inner product Let W = P2 be the subspace of quadratic polynomials. (a) Write down the conditions that a polynomial p P(4) must...

Let {v1 ( ( ( ( ( v} be an orthogonal basis for and let W = span (v1( ( ( ( ( vn). Is it necessarily true that W = span(vk+1( ( ( ( (vn)? Either prove that it is true or find a counterexample. R"

Find an orthogonal basis for that contains the vector 315

(B) Construct an ERD for a used car shop. A salesman will buy and sell cars. A client can either buy or sell their car. Please assign only 3 attributes per entity/relationship. Identify the primary...

THE UNIVERSITY OF NEW SOUTH WALES SCHOOL OF MATHEMATICS AND STATISTICS JUNE 2015 MATH2501 Linear Algebra (1) TIME ALLOWED - THREE HOURS. (2) TOTAL NUMBER OF QUESTIONS - 5 (3) ANSWER ALL QUESTIONS (4)...

THE UNIVERSITY OF NEW SOUTH WALES SCHOOL OF MATHEMATICS AND STATISTICS JUNE 2016 MATH2501 Linear Algebra (1) TIME ALLOWED - THREE HOURS. (2) TOTAL NUMBER OF QUESTIONS - 5 (3) ANSWER ALL QUESTIONS (4)...

Exercise 1: In lesson 12, we have seen that the set S = {po, P1, P2}, Po(x) = 1, P1(2) = = x, P2(20) (1 32), is an orthogonal set. 1. Find the norms of po, P and P2. 2. Let f(x) = e". Find the...

Let P3 have the inner product given by evaluation at 5 1 1 and 5 Let Po t 1 p t 3t and q t 13 Notice that these polynomials form an 12 orthogonal set with this inner product Find the best...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

PROBLEM 1 In the vector space V = I?\" of polynomials of degree S 2, Let W = {p I p} = 2p'(])} (where p'] is the derivative of p evaluated at 1) a) Show Wis a subspace of P2. b) Find a basis for W....

Indicate whether the following items are "Included in" or "Excluded from" gross income. a. Alimony payments received (relates to a divorce settlement in 2016). b. Damages award received by the...

- Find the points of intersection of curves y =3x +9 and y = 2x - 5x +3. y = 2x

Evaluate the integral. ( Use C for the constant of integration. ) x x 2 - 7 2 d x

Performance Bike Co. is a wholesaler of motorcycle supplies. An aging of the company's accounts receivable on December 31 and a historical analysis of the percentage of uncollectible accounts in each...

For each of the following, indicate whether the statement relates to managerial accounting (MA) or financial accounting (FA): a. Helps investors make investment decisions. b. Provides detailed...

Selected unadjusted account balances at December 31, 2014, are shown below for Demron Servicing. Required a. Demron estimates that 1.5% of net credit sales will prove to be uncollectible. Prepare the...

At January 1, 2018, NCI Industries, Inc., was indebted to First Federal Bank under a $240,000, 10% unsecured note. The note was signed January 1, 2014, and was due December 31, 2019. Annual interest...

Prepare the current asset section based on the following alphabetized post-closing trial balance information at March 31, 2014, for Whiteagle Company: Account Accounts payable Accounts receivable...

Which of the following is an example of an internal environment?CurrencyHuman resourcesCultureMode of entry

Show that each of the following sets of vectors is independent. (a) {x2, x + 1, 1 - x - x2} in P2 (b) 11][0 1] [1 0111 0 1 1 in M22

A wind is blowing from the south at 75 knots, and an airplane flies heading east at 100 knots. Find the resulting velocity of the airplane.

Given S and T in L(V, W), show that: (a) ker S ker T ker(S + T) (b) im(S + T) imS + im T

Suppose that 50% of the overnight parcels are sent via express mail service E2 and the remaining 10% are sent via E3. Of those sent via E2, only 1% arrive late, whereas 5% of the parcels handled by...

One method used to distinguish between granitic (G) and basaltic (B) rocks is to examine a portion of the infrared spectrum of the suns energy reflected from the rock surface. Let R1, R2, and R3...

One satellite is scheduled to be launched from Cape Canaveral in Florida, and another launching is scheduled for Vandenberg Air Force Base in California. Let A denote the event that the Vandenberg...