IN PYTHON please. Suppose youre in charge of picking a set of experiments to be launched into space. Each experiment has an ID number, an associated equipment mass in kilograms, and a value rating that approximates how important to science the collected data will be. Heres the set E of all experiments:

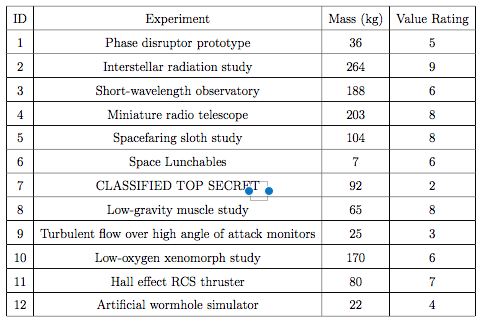
Unfortunately, not all of the experiments can be flown due to mass constraints theres only a certain amount of payload available for the experiments. Launching stuff into orbit is expensive!1 Thus, the challenge is to pick the subset of E whose elements have the highest possible combined value rating but at the same time dont exceed the payload capacity of your launch vehicle. This is an example of a constrained optimization problem.

One way to solve this problem is with a brute force approach. Consider all subsets of E. For each subset, determine its overall mass and value rating. Keep track of the highest-value subset with a combined mass within your vehicles payload capacity. Once all the subsets are considered, this highest-value subset is the one that should be flown.

Each experiment (row in the table) can be represented in Python as a list of three elements: the ID number, mass, and value rating. The first row, for example, can be stored as the list[1, 36, 5]. The entire set of experiments can then be represented as a list of these lists (i.e., a 2D list).

Write a Python function find optimal subset(E, m) that solves this optimization problem. The parameter E is a 2D list formatted as described above, and the parameter m is the max- imum payload capacity of your launch vehicle. The function should return a list containing three elements:

• Index 0 is the subset of E that provides the maximum possible combined value rating, without exceeding the payload limit m (this will be a list of lists, where each individual list corresponds to one experiment from E)

• Index 1 is the combined mass of that subset

• Index 2 is the combined value rating of that subset

Call your power set function as needed. Note that find optimal subset should work for anylist E formatted this way dont hard-code the values from the table into the function.

This is my power set function, if it needs to be edited then I understand but I am hoping I got that right :

def power_set(S):

if len(S) == 0: return [[]] x = S[-1] result = power_set(S[:-1]) copyResult = copy.deepcopy(result)

for c in copyResult: c.append(x) return result + copyResult

print(power_set([1, 2, 3]))

ID Mass (kg) Value Rating 1 36 5 2 264 9 3 188 6 4 203 8 5 104 8 6 Experiment Phase disruptor prototype Interstellar radiation study Short-wavelength observatory Miniature radio telescope Spacefaring sloth study Space Lunchables CLASSIFIED TOP SECRET Low-gravity muscle study Turbulent flow over high angle of attack monitors Low-oxygen xenomorph study Hall effect RCS thruster Artificial wormhole simulator 7 6 7 92 2 8 65 8 9 25 3 10 170 6 11 80 7 12 22 4