In the code below,

a) Modify it code to include interaction with the user by asking the user for the number of iterations that should be performed to estimate Pi. Add output to the code that prints the difference between the actual value of Pi and your estimate along with the number of iterations. Formulate the output as a single string.

b) Now increase the number of random numbers you use, by factors of 10, for a minimum of 5 steps. Observe what happens with the approximation of Pi. By what factor do you have to increase the number of iterations to get one more correct digit after the radix point? Keep track of the result and either plot it using Python (not necessary at this point), or by hand using a scatterplot showing the number of digits produced correctly on the y axis and the number of iterations on the x axis).

The code is

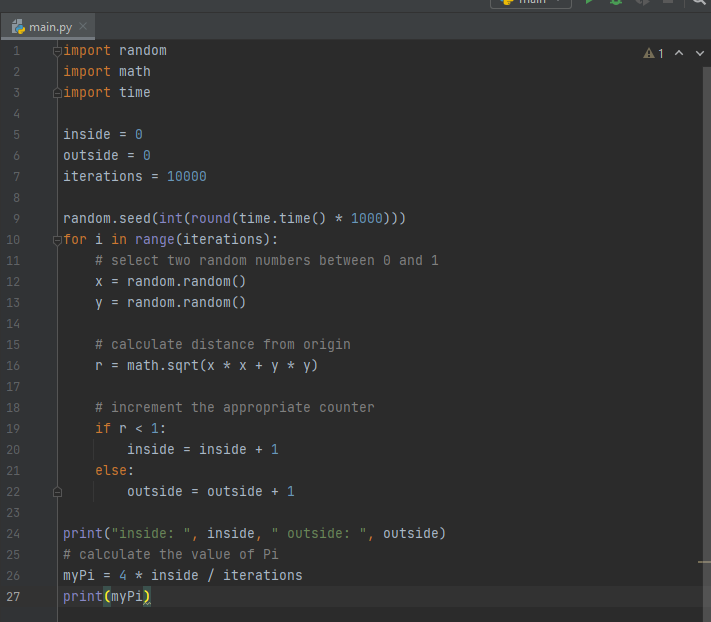
or in text

import random import math import time inside = 0 outside = 0 iterations = 10000 random.seed(int(round(time.time() * 1000))) for i in range(iterations): # select two random numbers between 0 and 1 x = random.random() y = random.random() # calculate distance from origin r = math.sqrt(x * x + y * y) # increment the appropriate counter if r   to main.py -import random 2. import math 3 import time A1 AV 4 5 6 inside = 0 outside iterations 7 = 10000 8 9 10 11 random.seed (int(round(time.time() * 1000))) for i in range(iterations): # select two random numbers between 0 and 1 x = random.random() y = random.random() 12 13 14 15 # calculate distance from origin r = math.sqrt(x * x + y * y) 16 17 18 19 20 # increment the appropriate counter if r