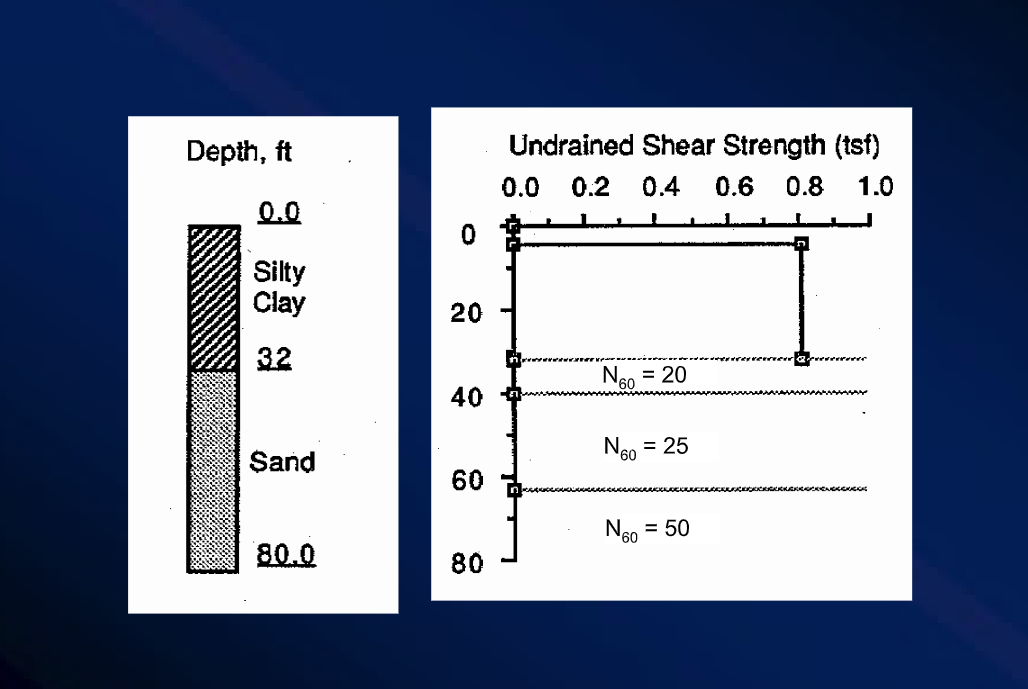
In the drilled shaft design example $9-6,$ the design load is now increased to $200$ tons. What will

be the shaft length $(30$ points$)?$ What is the settlement under load of $250$ tons $(20$ points$)?$

In the example, beta $(\backslash$beta $)$ is used to calculate side resistance in sand. Now, a different method is

proposed for unit side resistance in sand as follows $($NHI Course No$.132014,13\mathrm{.}3\mathrm{.}5\mathrm{.}1$

Cohesionless Soils$).$

$\backslash$beta ~~$(1-$sin$\backslash$phi $^(\text{'}))((\backslash$sigma $\_($p$)^(\text{'}))/(\backslash$sigma $\_($v$)^(\text{'})))^($sin$\backslash$phi $^(\text{'}))$tan$\backslash$phi $^(\text{'})$

Where both $\backslash$phi $^(\text{'})$ and $\backslash$sigma $\_($p$)^(\text{'})$ are evaluated, most commonly, by correlation to SPT N$-$values.

$\backslash$sigma $\_($p$)^(\text{'})=$ effective vertical pre$-$consolidation stress, which can be calculated as

$(\backslash$sigma $\_($p$)^(\text{'}))/($p$\_($a$))$~~$0\mathrm{.}47($N$\_(60))^($m$)$

$,$ m$=0\mathrm{.}8$ for silty sands, the sand in example $9-6.$

p$\_($a$)$ is atmospheric pressure; $\backslash$sigma $\_($v$)^(\text{'})=$ effective vertical over$-$burden pressure.

You may choose a method to estimate $\backslash$phi $^(\text{'})$ from measured SPT N$-$values.

The equation below is the recommended correlation for estimating $\backslash$phi $^(\text{'})$ for the purpose of

evaluating unit side resistance of drilled shafts in cohesionless soils.

$\backslash$phi $^(\text{'})=27\mathrm{.}5+9\mathrm{.}2$log$[($N$\_(1))\_(60)]$

Use alpha method for clay, and use both beta methods $($the one in the example and this new one$)$

for sand. Compare the side resistance by both beta methods. The ultimate resistance of your

drilled shaft shall be no more than $50$ tons higher than the required ultimate resistance.

Please clearly explain your steps, formula, design char$($t$)/($t$)$able $($if any$),$ and references.