In the graph shown in (a) comprising nodes 'A' through 'E', we assume that the players red and green take turns to move into one of the adjacent nodes at any single turn. The state of the game can be denoted by an ordered pair of letters. For example, the initial state of the game in (a) can be specified as 'AC', and after green's move to the 'E', the state becomes as 'EC'. The game ends only when the players are on the same node. The cost of each turn for player green is one, hence, the utility value of a terminal node SS (denotes as v(S)v(S)) for the green player is the minus of total turns taken until SS. The game is assumed to be zero-sum. From the initial state in (a), the green player starts first and the game follows afterward resulting in the partial game tree in the panel (b).

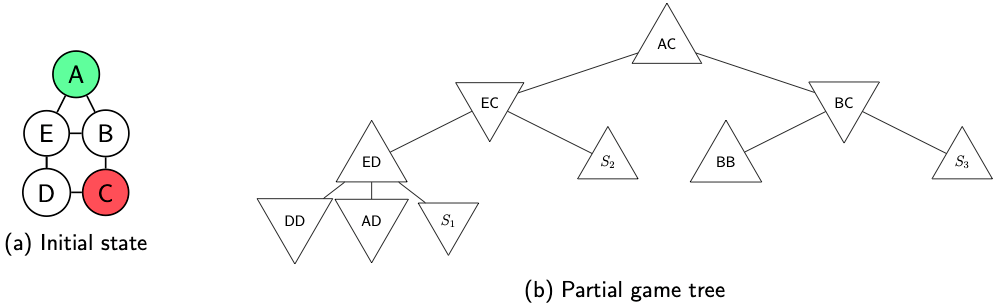
A. Follow the game tree in (b) and specify the states denoted by:

S1

S2

S3

B. Specify the terminal utility values of:

v(DD)

v(BB)

C. Without further expanding the game tree, specify the possible range of utility values for v(S_1)v(S1), v(S_2)v(S2), and v(S_3)v(S3), and propagate them to obtain v(AC)v(AC) (Hint: consider the least cost of the shortest paths on the graph until the game is finished.)

v(S1)

v(S2)=

v(S3)

v(AC)=

D. If the branches were considered for the left to right, which utility value could be discarded from further evaluation?

AC A EC BC E B ED S BB S3 DD AD Si (a) Initial state (b) Partial game tree