Question: In the next two problems, we receive an order from our partner aircraft manufacturing company, to design and fabricate a composite plate. In Problem 1
In the next two problems, we receive an order from our partner aircraft manufacturing company,
to design and fabricate a composite plate. In Problem we design and fabricate the composite,
and in Problem we test the quality of fabricated product.
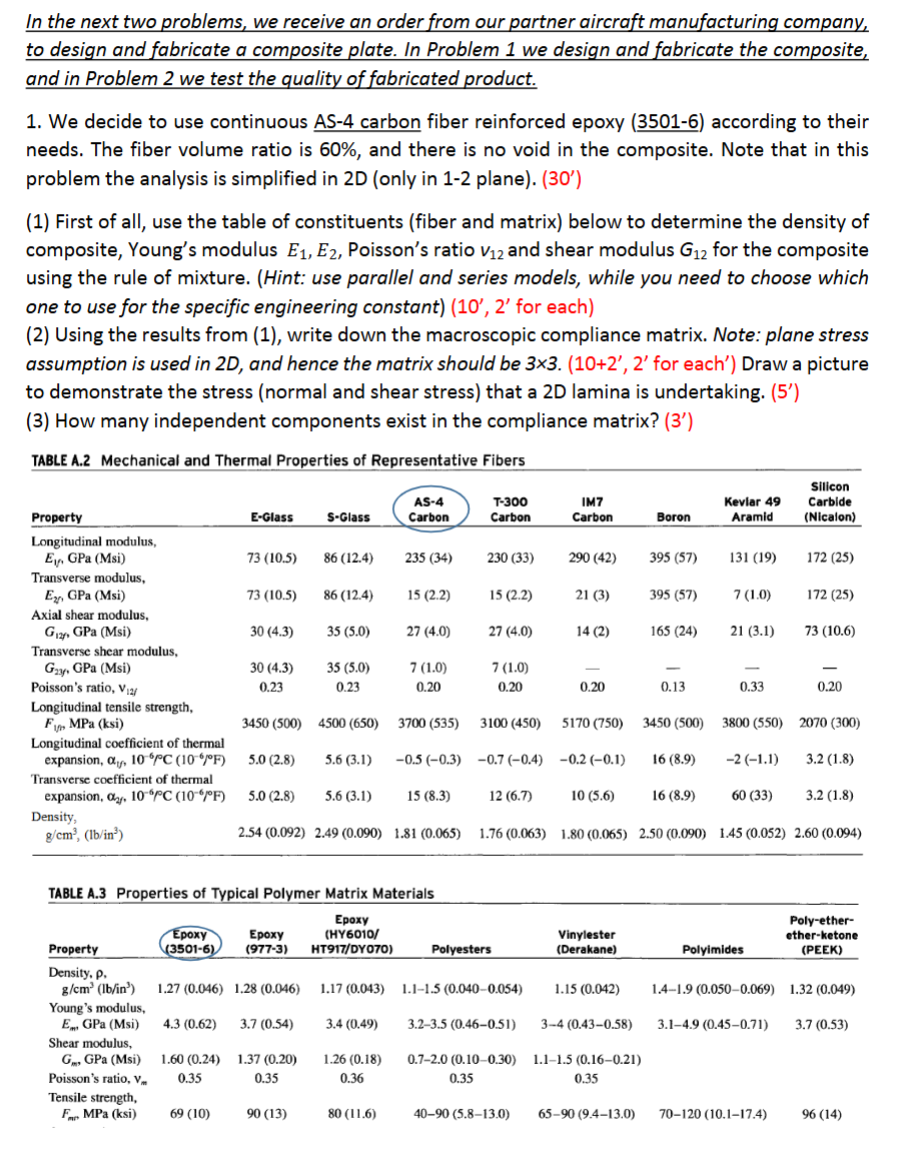
We decide to use continuous AS carbon fiber reinforced epoxy according to their
needs. The fiber volume ratio is and there is no void in the composite. Note that in this
problem the analysis is simplified in D only in plane
First of all, use the table of constituents fiber and matrix below to determine the density of
composite, Youngs modulus Poissons ratio and shear modulus G for the composite
using the rule of mixture. Hint: use parallel and series models, while you need to choose which
one to use for the specific engineering constant for each
Using the results from write down the macroscopic compliance matrix. Note: plane stress
assumption is used in D and hence the matrix should be for each Draw a picture
to demonstrate the stress normal and shear stress that a D lamina is undertaking.
How many independent components exist in the compliance matrix?
In the next two problems, we receive an order from our partner aircraft manufacturing company,
to design and fabricate a composite plate. In Problem we design and fabricate the composite,
and in Problem we test the quality of fabricated product.
We decide to use continuous AS carbon fiber reinforced epoxy according to their
needs. The fiber volume ratio is and there is no void in the composite. Note that in this
problem the analysis is simplified in D only in plane
First of all, use the table of constituents fiber and matrix below to determine the density of
composite, Young's modulus EE Poisson's ratio v and shear modulus G for the composite
using the rule of mixture. Hint: use parallel and series models, while you need to choose which
one to use for the specific engineering constant for each
Using the results from write down the macroscopic compliance matrix. Note: plane stress
assumption is used in D and hence the matrix should be x for each' Draw a picture
to demonstrate the stress normal and shear stress that a D lamina is undertaking.
How many independent components exist in the compliance matrix?
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


