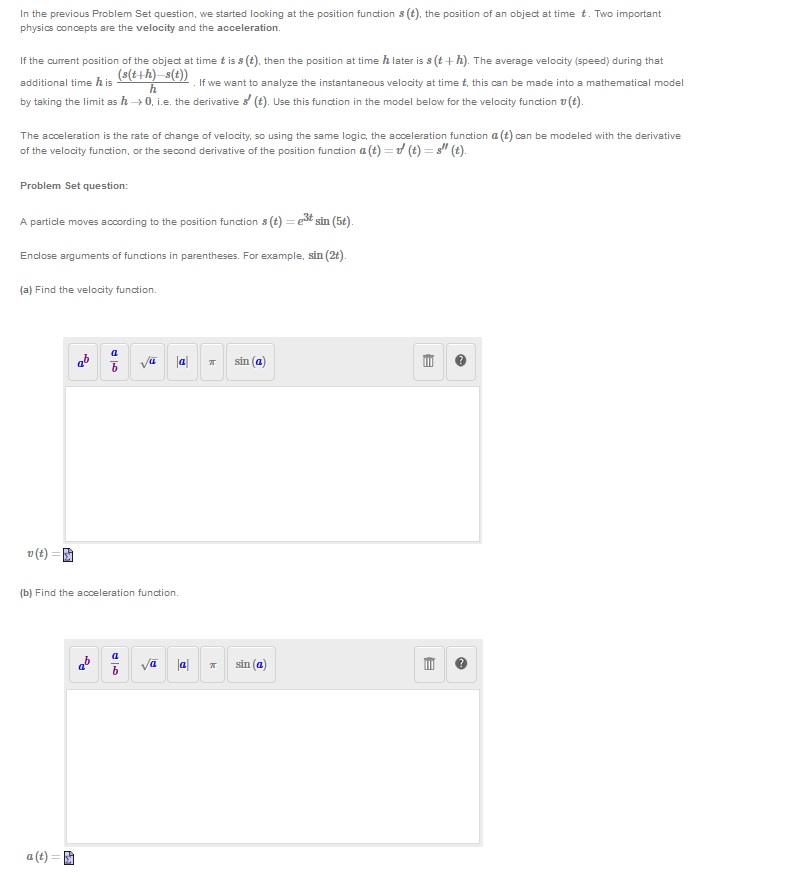
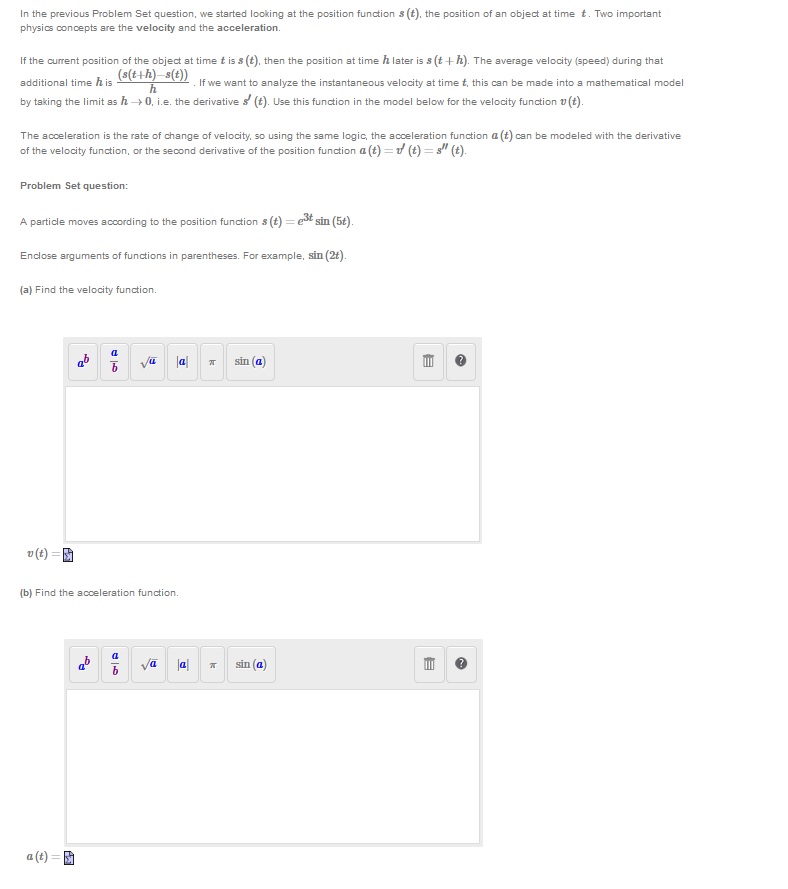
In the previous Problem Set question, we started looking at the position function s (t), the position of an object at time t. Two important physics concepts are the velocity and the acceleration. If the current position of the object at time t is $ (t), then the position at time / later is $ (t + h). The average velocity (speed) during that additional time his ((th)- s()) . If we want to analyze the instantaneous velocity at time t, this can be made into a mathematical model by taking the limit as h -> 0, i.e. the derivative s' (t). Use this function in the model below for the velocity function u (t) The acceleration is the rate of change of velocity. so using the same logic, the acceleration function a (t) can be modeled with the derivative of the velocity function, or the second derivative of the position function a (t) = (t) = s" (t). Problem Set question: A particle moves according to the position function s (t) = est sin (5#). Enclose arguments of functions in parentheses. For example, sin (2t). (a) Find the velocity function. sin (a) ? D (t) = (b) Find the acceleration function. sin (a) ? a (t) =