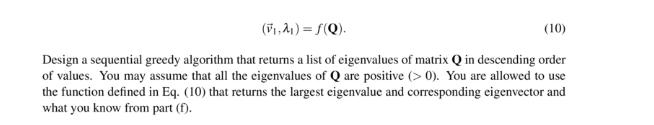
In the real world, it is not computationally practical to directly solve for the eigenbasis for large matrices as you might do for small matrices on paper. You need to build an algorithm that sequentially computes the eigenbasis for a square symmetric matrix Q = ATA (Note: Any matrix that can be written with A RNXN in this form is symmetric). To accomplish this we are given access to a function, (V, 2) = f(Q), that returns the largest eigenvalue of the matrix Q and the corresponding eigenvector. We will use this function to build a sequential greedy algorithm (similar to Orthogonal Matching Pursuit) that computes the eigenvectors and eigenvalues in descending order. IMPORTANT: Throughout the problem, you should assume that the magnitude of each eigenvector is 1 (i.e. ||||= 1), that the eigenvalues are real, unique, and distinct, and that A > A >> AN > 0. (a) Show that the matrix Q = AT A is symmetric (i.e. Q =Q) when, A = 12 3 (2) (b) Given two distinct eigenvalue/eigenvector pairs, (2.) and (2.ve). show that for the symmetric matrix Q = A' A, if Athen (v.) = 0 (i.e. any pair of eigenvectors with distinct eigenvalues is orthogonal). Hint: Consider: QUk = 2k V/Q=dev. (c) Let us consider V to be an orthonormal matrix, where -44-9 (3) (5) Show that if V is an orthonormal matrix, then VTV = I. (d) Recall that the columns of orthonormal matrix V form a basis for RN, as you proved in the discussion sections. Assume a= [a... a represents in the basis of V. Find (v,,.). VN. Hint: Write x as a linear combination of the column vectors V, (e) Let us define, V(2) +4 Assume a = [a...an] represents in the basis of V. Find , the projection of a vectorERN onto the columns of the orthonormal matrix V(2): (6) =projcl(v() (*). What is the magnitude of the error vector, -x? (f) We know that because Q is symmetric, V is an orthonormal matrix. We use the idea of diagonalization and part (c) of the problem to express Q as: Q=A'A=VAV = VAVT = [ A= 20 0 0 2 0 0 023 : 0 0 0 *** 0 0 0 AN (8) (9) Let Q2Q-A. Thus, Q(2) represents Q after the component associated with direction v is removed. Show that is in the null space of Q(2). Hint: Can you write Q(2) using Eq. (8)? (g) Recall the function that returns the largest eigenvalue and corresponding eigenvector of a matrix, (7) (F,2) = S(Q). (10) Design a sequential greedy algorithm that returns a list of eigenvalues of matrix Q in descending order of values. You may assume that all the eigenvalues of Q are positive (>0). You are allowed to use the function defined in Eq. (10) that returns the largest eigenvalue and corresponding eigenvector and what you know from part (f).