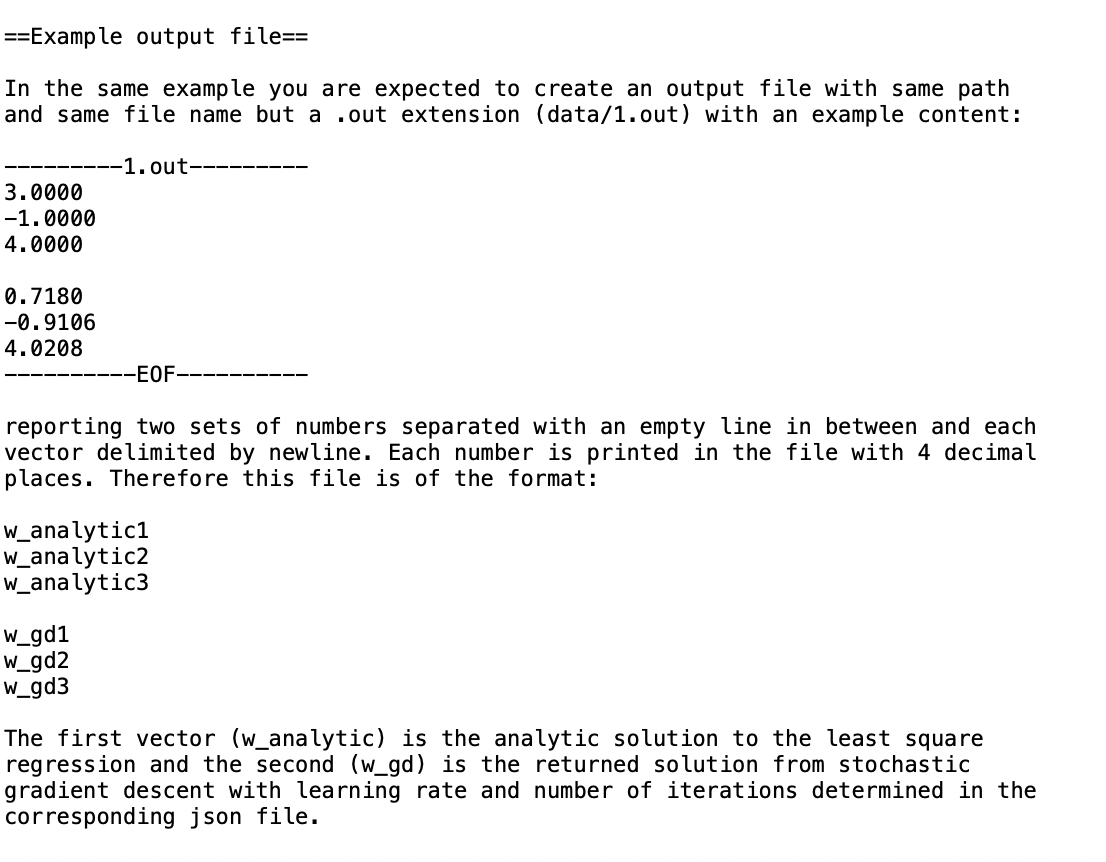
In this assignment you implement a simple least square fitting using both the analytic solution and stochastic gradient descent. ==Example input file== In example data/1. in the file contains the lines ------1. in----- 14 20 69 16 3 -1 24 30 99 11 62 240 30 -4 -43 ----------EOF---------- which should be interpreted as a training dataset of 5 samples (x, y) where x is a two-dimensional real vector x = (x1, x2). Therefore each line of 1.in is of the format: x1 x2 y ==Example output file== In the same example you are expected to create an output file with same path and same file name but a .out extension (data/1.out) with an example content: ---------1.out----- 3.0000 -1.0000 4.0000 0.7180 -0.9106 4.0208 -------EOF------ reporting two sets of numbers separated with an empty line in between and each vector delimited by newline. Each number is printed in the file with 4 decimal places. Therefore this file is of the format: W_analytic1 W_analytic2 w_analytic3 W_gd1 W_gd2 W_gd3 The first vector (w_analytic) is the analytic solution to the least square regression and the second (w_gd) is the returned solution from stochastic gradient descent with learning rate and number of iterations determined in the corresponding json file. ==Example json file== The json file is a python dictionary with choices of the above-mentioned hyperparameters. Depending on your implementation good choice of hyperparameters might be different from these example values. By trial and error modify these values so that your stochastic gradient descent produces results as close as possible to the analytic solution. ----1. json--- "learning rate": 0.0001, "num iter": 1000 ------EOF------ In this assignment you implement a simple least square fitting using both the analytic solution and stochastic gradient descent. ==Example input file== In example data/1. in the file contains the lines ------1. in----- 14 20 69 16 3 -1 24 30 99 11 62 240 30 -4 -43 ----------EOF---------- which should be interpreted as a training dataset of 5 samples (x, y) where x is a two-dimensional real vector x = (x1, x2). Therefore each line of 1.in is of the format: x1 x2 y ==Example output file== In the same example you are expected to create an output file with same path and same file name but a .out extension (data/1.out) with an example content: ---------1.out----- 3.0000 -1.0000 4.0000 0.7180 -0.9106 4.0208 -------EOF------ reporting two sets of numbers separated with an empty line in between and each vector delimited by newline. Each number is printed in the file with 4 decimal places. Therefore this file is of the format: W_analytic1 W_analytic2 w_analytic3 W_gd1 W_gd2 W_gd3 The first vector (w_analytic) is the analytic solution to the least square regression and the second (w_gd) is the returned solution from stochastic gradient descent with learning rate and number of iterations determined in the corresponding json file. ==Example json file== The json file is a python dictionary with choices of the above-mentioned hyperparameters. Depending on your implementation good choice of hyperparameters might be different from these example values. By trial and error modify these values so that your stochastic gradient descent produces results as close as possible to the analytic solution. ----1. json--- "learning rate": 0.0001, "num iter": 1000 ------EOF