In this assignment, you'll apply these same ideas to calculate derivatives using two finite difference formulas; and you'll also learn the importance of mesh size in determining the accuracy of these calculations.

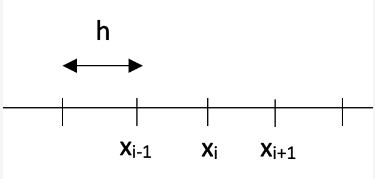
To simplify, let's assume that we're working with a uniform one-dimensional mesh, with the distance between adjacent nodes being the "mesh size" h.

Thus,

xi+1=xi+h

and

xi?1=xi?h

Knowing the value of a function f at each node in the mesh, your objective is to calculate the derivative of f at node x_i.

To derive the two formulas you'll be using, we start with the definition of the derivative:

f?(x)=Limh?0f(x+h)?f(x)h

If we applied this formula to our grid values, we would get theforward differenceexpression

f?(xi)?f(xi+1)?f(xi)h

and thebackward differenceexpression

f?(xi)?f(xi)?f(xi?1)h

Note that these are approximations to the value of the derivative, since we're not taking the limit as h goes to zero; but we can improve the approximation by taking the average of these two difference formulas:

f?(xi)?12(f(xi+1)?f(xi)h+f(xi)?f(xi?1)h)

which simplifies to thecentered differenceexpression

f?(xi)?f(xi+1)?f(xi?1)2h

With this background, here's your assignment:

• Assume the function f is defined as f(x) = 5x⁴- 9x³+ 2
• Use the power rule to find the derivative f'(x) and evaluate that derivative at x = 1.7. Note:To avoid round-off error, retain at least six decimal places in your calculations.
• Use the "forward difference" and "centered difference" formulas to estimate f'(x) at x = 1.7 for three different values of the mesh sizes
  • h = 0.1
  • h = 0.01
  • h = 0.001
• Use your calculated values to fill in this table:

h	forward difference approximation	centered difference approximation	exact derivative
0.1
0.01
0.001

• Answer the following two questions:
  • Which formula yields a better approximation: The forward difference or the centered difference?
  • What effect does reducing the mesh size h have upon the accuracy of these approximations?

Be sure to show all of your work in making these calculations.

\f