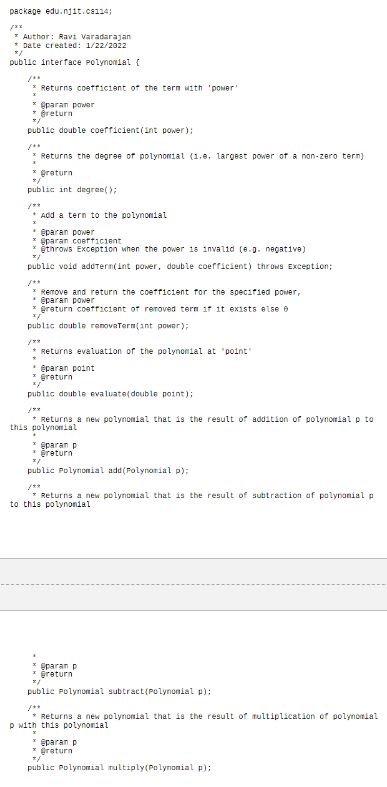
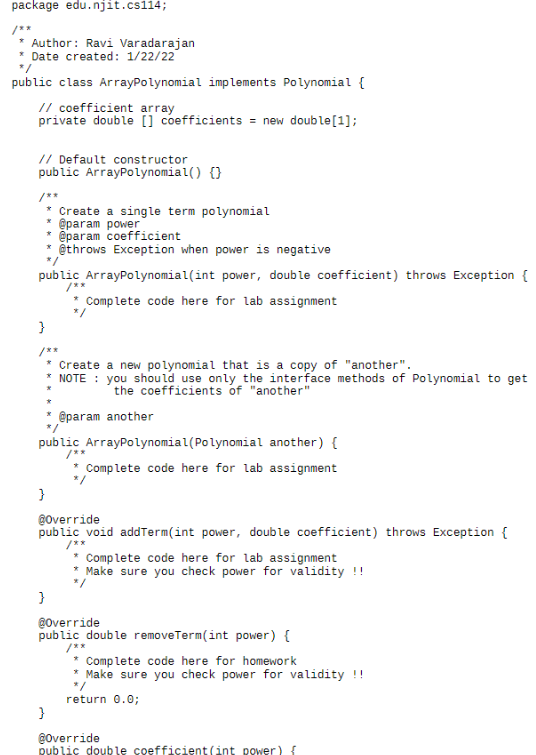
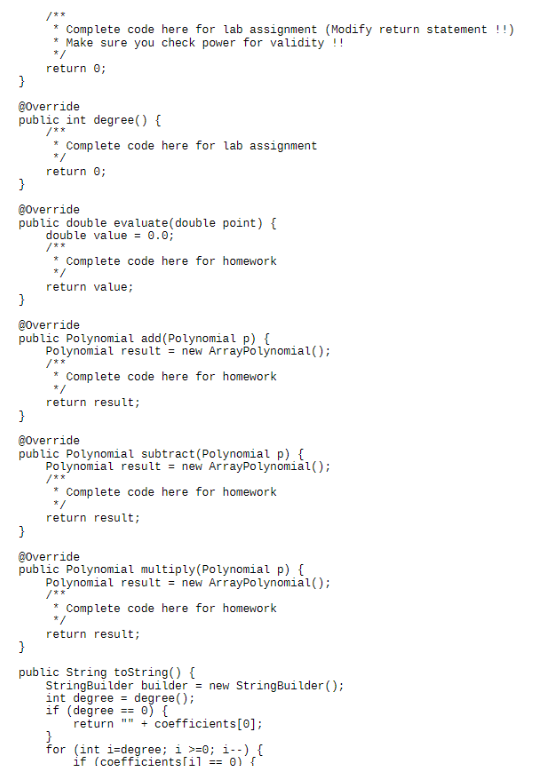
In this lab assignment, you will be implementing a part of ArrayPloynomial.java that is a specific implementation of Polynomial ADT mentioned in homework assignment 1. In this implementation, you will be using an array to store the coefficients where the k-th position in the array contains coefficient of xk in the polynomial. It will be zero if xk term does not exist in the polynomial. Note that the degree of a polynomial is the highest power of a non-zero term in the polynomial. The coefficient array is initialized to an array of length 1 to represent a zero polynomial. The array will expand to accommodate terms higher than the degree of the polynomial. The array can optionally shrink when remove Term() causes the degree of the polynomial to decrease. You are provided a starter file for ArrayPolynomial.java with data members defined. You need to complete the following (non-default) constructors: public ArrayPolynomial (int power, double coefficient) throws Exception {.... } public ArrayPolynomial (Polynomial another) {.. } You also need to complete the following functions: public void addTerm(int power, double coefficient) throws Exception {.. } public double coefficient(int power) {...} public int degree () {.. } I suggest you complete these in the following order: degree(), coefficient(), addTerm(), constructors Make sure you run ArrayPolynomial.java with the JVM option "-ea" in order to enable assertions. Otherwise you may not get any exceptions even if an assertion condition fails. package edu.nit.08124; Author: Ravi Varadarajan Date created: 1/22/2022 public interface polynomial { x * Returns coefficient of the term with 'power @parar power * @return 21 public double coefficient(int power); * Returns the degree of polynomial (1.6. largest power of a non-zero tern) * return public int degree(); /** * Add a tern to the polynomial * @paran power * @paran coefficient throws Exception when the power is invalid (e... negative) public void addTern(int power, double coefficient) throws Exception; * Remove and return the coefficient for the specified power, eparan power * @return coefficient of removed term if it exists else public double renoveTerm(int power); + Returns evaluation of the polynomial at point @paran point greturn public double evaluate double point); * Returns a new polynomial that is the result of addition of polynomial p to this polynomial * paran return */ public Polynomial add(Polynomial p); * Returns a new polynomial that is the result of subtraction of polynomial to this polynonial eparan p return public Polynomial subtract(Polynomial p): * Returns a new polynomial that is the result of multiplication of polynomial p with this polynomial * @paran p return * public Polynomial multiply(Polynonial p); package edu.njit.cs114; * Author: Ravi Varadarajan * Date created: 1/22/22 public class ArrayPolynomial implements Polynomial { // coefficient array private double [] coefficients = new double[1]; // Default constructor public ArrayPolynomial() {} /** * Create a single term polynomial * @param power * @param coefficient * @throws Exception when power is negative public ArrayPolynomial(int power, double coefficient) throws Exception { Complete code here for lab assignment */ } /** * Create a new polynomial that is a copy of "another". NOTE : you should use only the interface methods of Polynomial to get the coefficients of "another" @param another public ArrayPolynomial(Polynomial another) { Complete code here for lab assignment } @Override public void addTerm(int power, double coefficient) throws Exception { Complete code here for lab assignment * Make sure you check power for validity !! } @Override public double removeTerm(int power) { /** * Complete code here for homework * Make sure you check power for validity !! return 0.0; } @Override public double coefficient (int power) Complete code here for lab assignment (Modify return statement !!) Make sure you check power for validity !! return 0; } @Override public int degree() { * Complete code here for lab assignment return 0; } @Override public double evaluate( double point) { double value = 0.0; * Complete code here for homework return value; ) @Override public Polynomial add(Polynomial p) { Polynomial result = new ArrayPolynomial(); * Complete code here for homework return result; } @Override public Polynomial subtract(Polynomial p) { Polynomial result = new ArrayPolynomial(); Complete code here for homework return result; } @Override public Polynomial multiply(Polynomial p) { Polynomial result = new ArrayPolynomial(); * Complete code here for homework */ return result; } public String toString() { StringBuilder builder = new StringBuilder(); int degree - degree(); if (degree == 0) { return + coefficients[0]; } for (int i=degree; i >=0; i--) { if (coefficientslil == 0) continue; if (i O? builder append(Math.abs(coefficients[:])); } else { busider.append(coefficients[:]); if (> 0) 1) builder append("A" - 1); return builder.toString(); 3 same * Returns true if the object obj is a Polynomial and its coefficients are the for all the terms in the polynomial @paran obj @return true or false @Override public boolean equals(Object obj) { if (!(obj instanceof Polynomial)) { return false; Polynomial other (Polynomial) obj; if (degree() other.degree()) { return false; 3 int degree degree(); for (int i=0; i