In this problem, we are going to have a simple hash function that can have a collision.

generate the hash function of an English word as follows:

Take the character $->$ Convert it to Binary Ascii $->1$ bit Right circular shift $->$ XoR with

$101010101->$ Take the right most bit

For example, lets say we have a word $$card$.$ We will convert this to a $4$ bit binary hash value as

follows:

c $->01100011($Ascii$)->10110001($right circular shift$)->00011011($xor with $10101010)->1$

$($right most bit$)$

a $->01100001($Ascii$)->10110000($right circular shift$)->00011010($xor with $10101010)->0$

$($right most bit$)$

r $->01110010($Ascii$)->00111001($right circular shift$)->10010011($xor with $10101010)->1$

$($right most bit$)$

d $->01100100($Ascii$)->00110010($right circular shift$)->10011000($xor with $10101010)->0$

$($right most bit$)$

So the final hash value of $$card$$ is $1010$

Since the final hash value is just $4$ bit long therefore, there might be multiple strings that will

produce the same hash value.

Find two different strings of length $4$ that will produce the same hash value using the above hash

function. You need to show the way you are computing the hash value. You will not get any

point if you just write down the two strings.

Part $2$

In your previous part, you constructed a hash value from a hash function. In this part, we are

going to construct a Merkle tree from a list of word. In Markle tree structure, we pair words,

computes the has values of each and then compute another hash value from the pair of hash

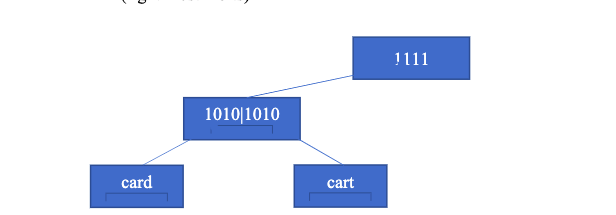
values. Lets say, we have two words $$card$$ and $$cart$$ and we can construct the Markle tree as

follows:

card $->1010($Hash value from previous part$)$

t $->01100100($Ascii$)->00110010($right circular shift$)->10011000($xor with $10101010)->0$

$($right most bit$)$

cart $->1010($Hash Value$)$

We will use a little bit different hash function while constructing the hash value for the upper

level of the tree. Markel Tree

card$|$cart $->10101010->01010101($right circular shift$)->11111111($xor with $10101010)\_->$

$1111($right most $4$ bits$)$

The construction is shown in the above diagram.

Using the above example as reference, construct a Merkle tree for the following words $,$

dump, lamp, fact, hand, send, lord, mask, aunt, park, dark, load, code, back, loss, yard, good

Lets say someone claim that the word lock should be there. What branch of the binary tree will

you disclose? Explain the calculation based on the branch you reveal and prove that the word

lock should not be there.

Lets say someone claim that the word dark should not be there. What branch of the binary tree

will you disclose? Explain the calculation based on the branch you reveal and prove that the word ock should not be there.

Lets say someone claim that the word dark should not be there. What branch of the binary tree

will you disclose? Explain the calculation based on the branch you reveal and prove that the word dark should be there.

Lets say someone claim that the word dark should not be there. What branch of the binary tree

will you disclose? Explain the calculation based on the branch you reveal and prove that the

word dark should be there.