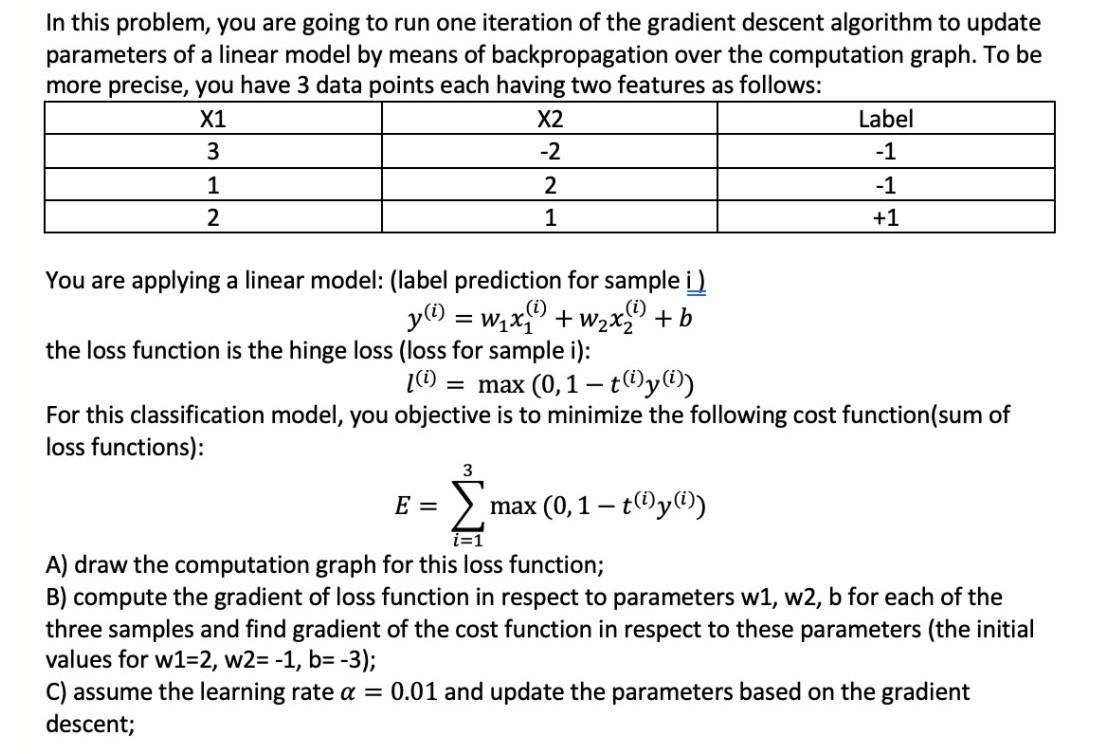
In this problem, you are going to run one iteration of the gradient descent algorithm to update parameters of a linear model by means of backpropagation over the computation graph. To be more precise, you have 3 data points each having two features as follows: X1 X2 Label 3 -2 -1 1 2 -1 2 1 +1 (i) = You are applying a linear model: (label prediction for sample i) y(t) = wax) + w2x + b the loss function is the hinge loss (loss for sample i): [0) = max (0,1 t(1)y(i)) For this classification model, you objective is to minimize the following cost function(sum of loss functions): 3 E= max (0,1 t(i)y(i)) A) draw the computation graph for this loss function; B) compute the gradient of loss function in respect to parameters w1, w2, b for each of the three samples and find gradient of the cost function in respect to these parameters (the initial values for w1=2, W2=-1, b=-3); C) assume the learning rate a = 0.01 and update the parameters based on the gradient descent