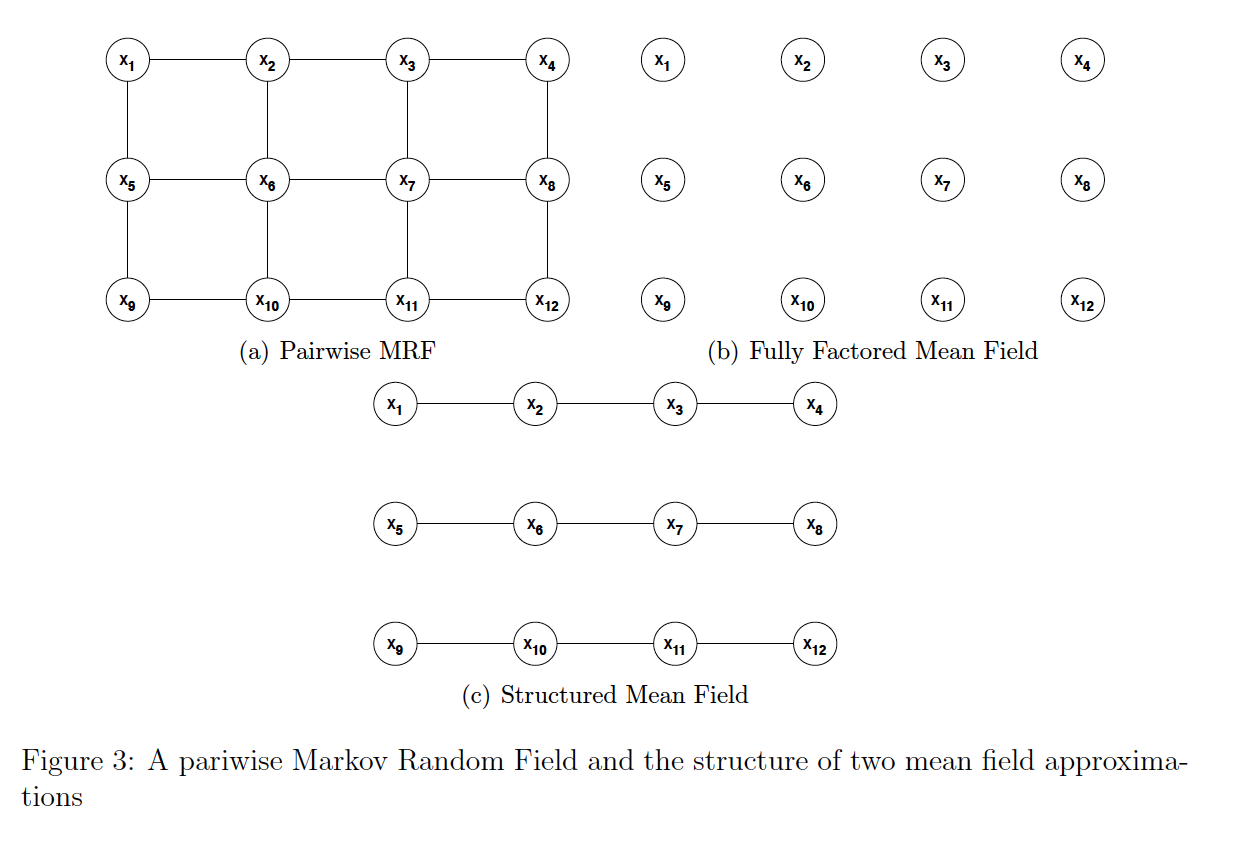
In this problem, you will investigate mean field approximate inference algorithms (Koller & Friedman 11.5). Consider the Markov network in Figure 3(a). Define edge potentials Oij (xi, xj) for all edges (xi, xj) in the graph. We can write P(x1,...,x12) = II j (x1,x;) i Z (i,j)E (a) Assume a fully factored mean field approximation Q (Figure 3(b)), parameterized by node potentials Qi. (i) Write down the update formula for Q1(x1). (ii) Write down the update formula for Q6(x6). In both cases, please expand out any expectations in the formulas (your answer should be in terms of Qi and oij). (b) Now we consider a structured mean field approximation Q (Figure 3(c)), parameterized by edge potentials Vij (xi, xj) for each edge (xi, xj) in Figure 3(c). (i) Write down the update formula for 12(x1, x2) up to a proportionality constant. This time, you can write it in terms of expected values, but do not include un- necessary terms. (ii) Write out the formula for Eq[In 23(X2, X3)|x1, x2]. Make sure to show how you would calculate the distribution that this expectation is over. (iii) Write out the formula for EQ [ln 15 (X1, X5)|x1, x2], Again, show how you would evaluate distribution Q. 4 X3 X2 X4 X3 X2 X X8 7 6 X5 X8 7 X6 X5 Xg g X12 X11 X10 (a) Pairwise MRF X3 X2 10 X11 (b) Fully Factored Mean Field X4 X8 x7 6 X5 X12 Xg 10 X11 (c) Structured Mean Field X12 Figure 3: A pariwise Markov Random Field and the structure of two mean field approxima- tions