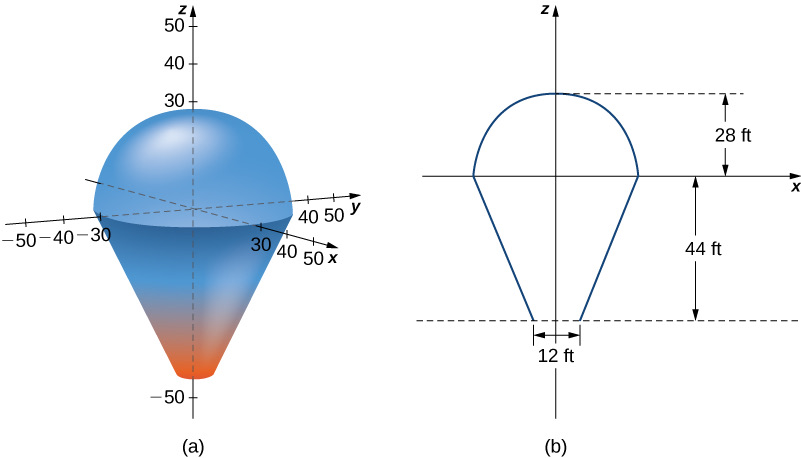
In this project we use triple integrals to learn more about hot air balloons. We model the balloon in two pieces. The top of the balloon is modeled by a half sphere of radius 28 feet. The bottom of the balloon is modeled by a frustum of a cone (think of an ice cream cone with the pointy end cut off). The radius of the large end of the frustum is 28 feet and the radius of the small end of the frustum is 6 feet. A graph of our balloon model and a cross-sectional diagram showing the dimensions are shown in the following figure.We first want to find the volume of the balloon. If we look at the top part and the bottom part of the balloon separately, we see that they are geometric solids with known volume formulas. However, it is still worthwhile to set up and evaluate the integrals we would need to find the volume. If we calculate the volume using integration, we can use the known volume formulas to check our answers. This will help ensure that we have the integrals set up correctly for the later, more complicated stages of the project.Find the volume of the balloon in two ways.Use triple integrals to calculate the volume. Consider each part of the balloon separately. (Consider using spherical coordinates for the top part and cylindrical coordinates for the bottom part.)Verify the answer using the formulas for the volume of a sphere, V=43?r3, and for the volume of a cone, V=13?r2h. In reality, calculating the temperature at a point inside the balloon is a tremendously complicated endeavor. In fact, an entire branch of physics (thermodynamics) is devoted to studying heat and temperature. For the purposes of this project, however, we are going to make some simplifying assumptions about how temperature varies from point to point within the balloon. Assume that just prior to liftoff, the temperature (in degrees Fahrenheit) of the air inside the balloon varies according to the functionT0(r,?,z)=(z?r)/10+210.

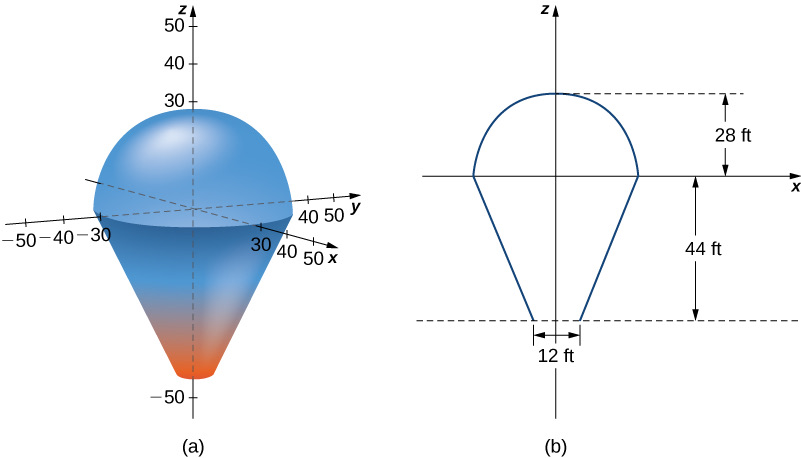
ZI ZA 50 40 30 28 ft 40 50 50-40-30 30 40 50 X 44 ft 12 ft 50 (a) (b )