In this project we use triple integrals to learn more about hot air balloons. We model the balloon in two pieces. The top of the balloon is modeled by a half sphere of radius 28 feet. The bottom of the balloon is modeled by a frustum of a cone (think of an ice cream cone with the pointy end cut off). The radius of the large end of the frustum is 28 feet and the radius of the small end of the frustum is 6 feet. A graph of our balloon model and a cross-sectional diagram showing the dimensions are shown in the following figure.What is the average temperature of the air in the balloon just prior to liftoff? (Again, look at each part of the balloon separately, and do not forget to convert the function into spherical coordinates when looking at the top part of the balloon.)Now the pilot activates the burner for 10 seconds. This action affects the temperature in a 12 -foot-wide column 20 feet high, directly above the burner. A cross section of the balloon depicting this column in shown in the following figure.Assume that after the pilot activates the burner for 10 seconds, the temperature of the air in the column described above increases according to the formulaH(r,?,z)=?2z?48.Then the temperature of the air in the column is given byT1(r,?,z)=(z?r)/10+210+(?2z?48),while the temperature in the remainder of the balloon is still given byT0(r,?,z)=(z?r)/10+210.

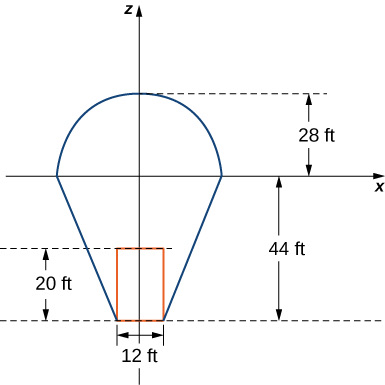
ZI 28 ft X 44 ft 20 ft 12 ft