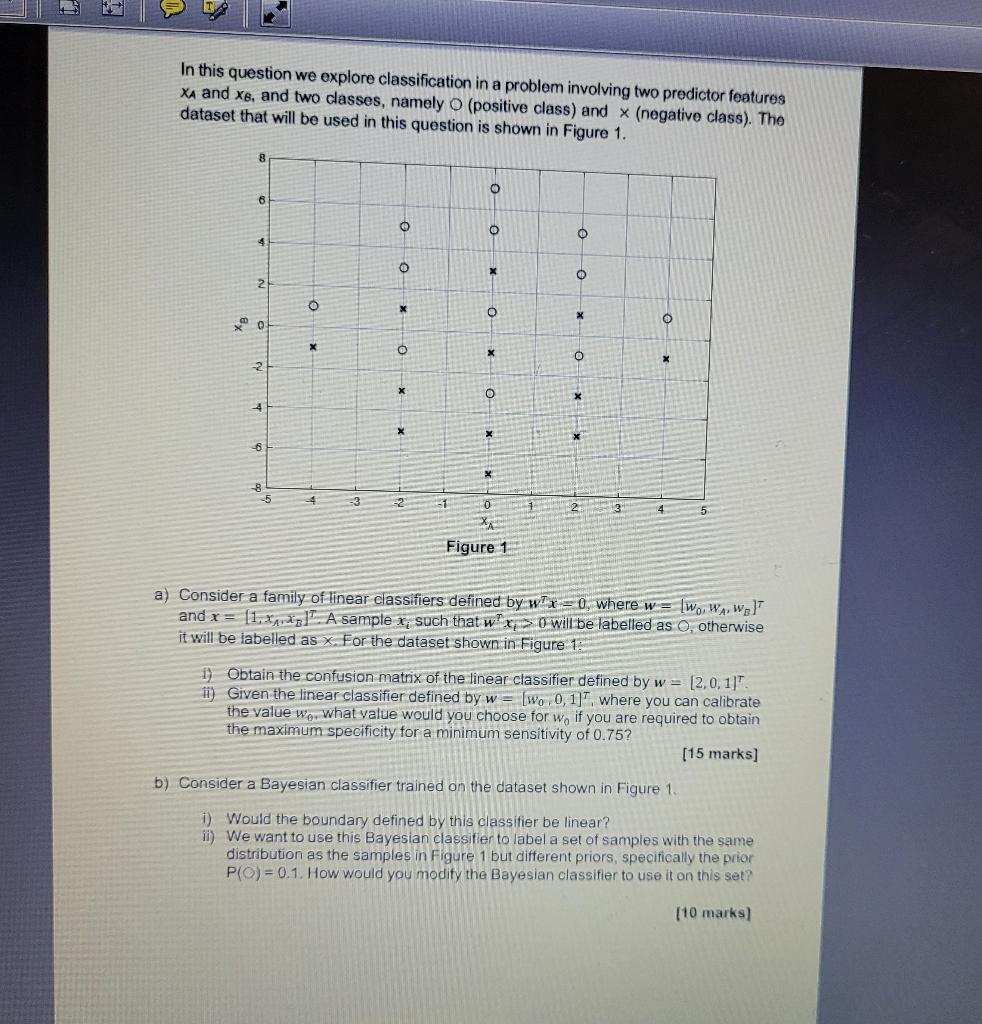
In this question we explore classification in a problem involving two predictor features xA and xB, and two classes, namely O (positive class) and x (negative class). The dataset that will be used in this question is shown in Figure 1. a) Consider a family of linear classifiers defined by wx=0, where w=[w0,wA,wB] and x=[1,xA,xB]. A sample xi such that wTxi>0 will be labelled as 0 , otherwise it will be labelled as x. For the dataset shown in Figure 1 . 1) Obtain the confusion matrix of the linear classifier defined by w=[2,0,1]. ii) Given the linear classifier defined by w=[w0,0,1]T, where you can calibrate the value w0, what value would you choose for w0 if you are required to obtain the maximum specificity for a minimum sensitivity of 0.75 ? [15 marks] b) Consider a Bayesian classifier trained on the dataset shown in Figure 1. i) Would the boundary defined by this classifier be linear? ii) We want to use this Bayesian classiter to label a set of samples with the same distribution as the samples in Figure 1 but different priors, specifically the prior P(O)=0.1. How would you modity the Bayesian classifier to use it on this set