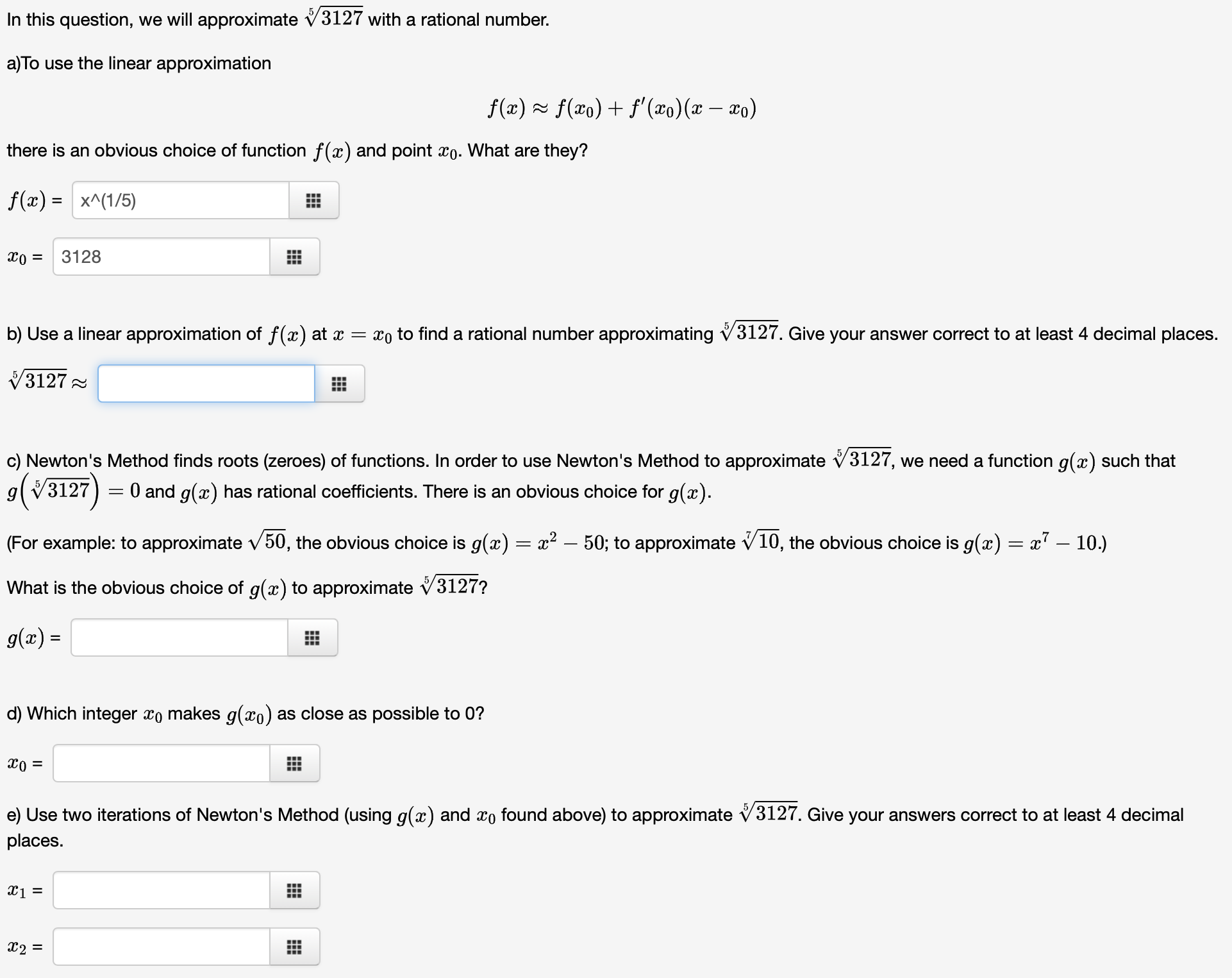
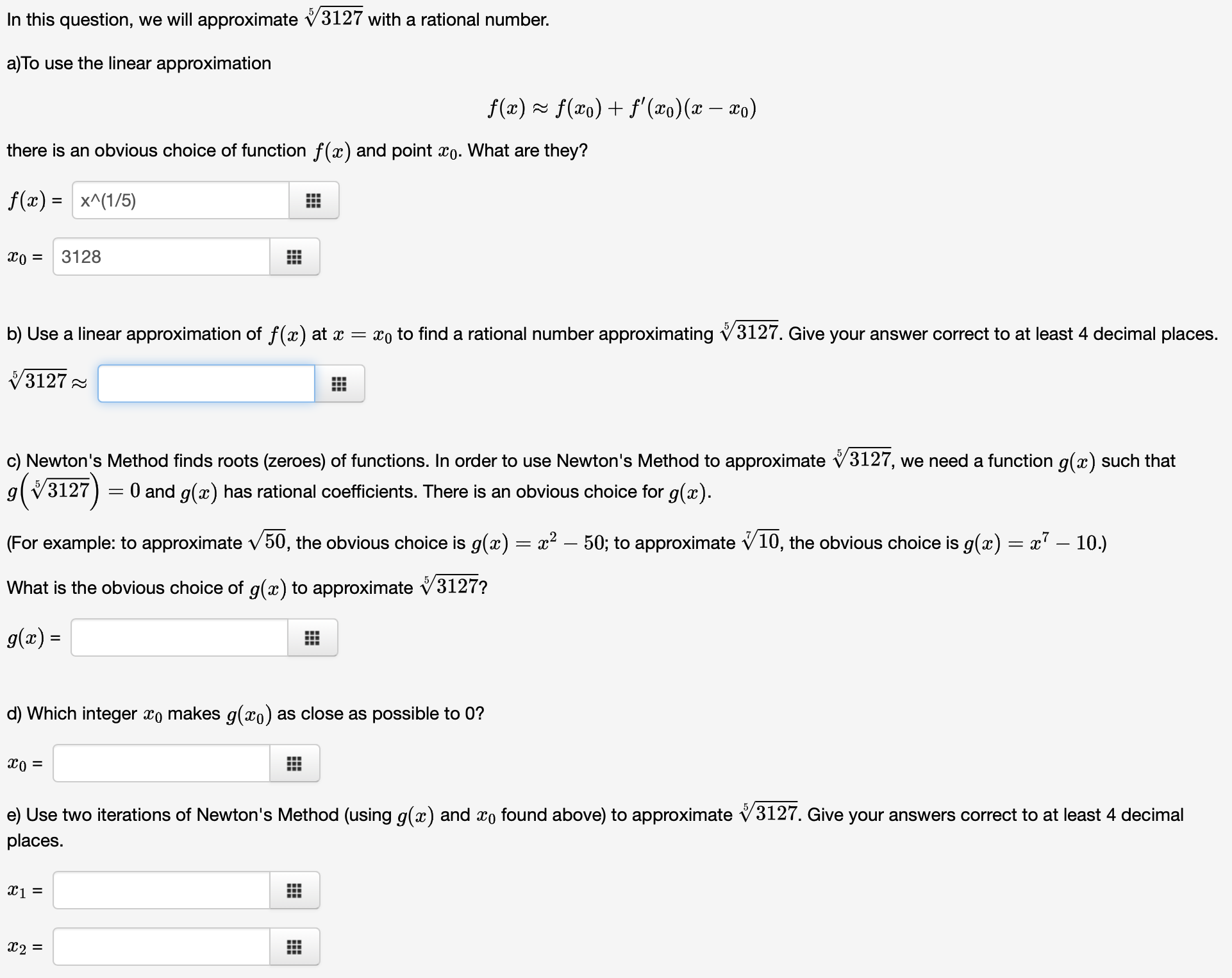
In this question, we will approximate V5 3127 with a rational number. a)To use the linear approximation f0\") R' f($o) + JCT-700M?\" 5130) there is an obvious choice of function f (w) and point .930. What are they? ax) = x"(1/5) iii :00 = 3128 555 b) Use a linear approximation of f (9:) at :c = {no to find a rational number approximating V5 3127. Give your answer correct to at least 4 decimal places. V5 3127a c) Newton's Method finds roots (zeroes) of functions. In order to use Newton's Method to approximate V5 3127, we need a function 9(32) such that g(\\/5 3127) = 0 and 9(93) has rational coefficients. There is an obvious choice for 9(a). (For example: to approximate V 50, the obvious choice is 9(3) 2 $2 50; to approximate V7 10, the obvious choice is g(a:) : $7 10.) What is the obvious choice of 9(33) to approximate V5 3127? 906) = 555 d) Which integer :50 makes g(m0) as close as possible to 0? 930 = 555 e) Use two iterations of Newton's Method (using g(:c) and :30 found above) to approximate V5 3127. Give your answers correct to at least 4 decimal places. 8 ,_. ll