Question: In this question, you will use your binary tree implementation from Quiz 5 to implement a set ADT. . First, you should have your binary_tree

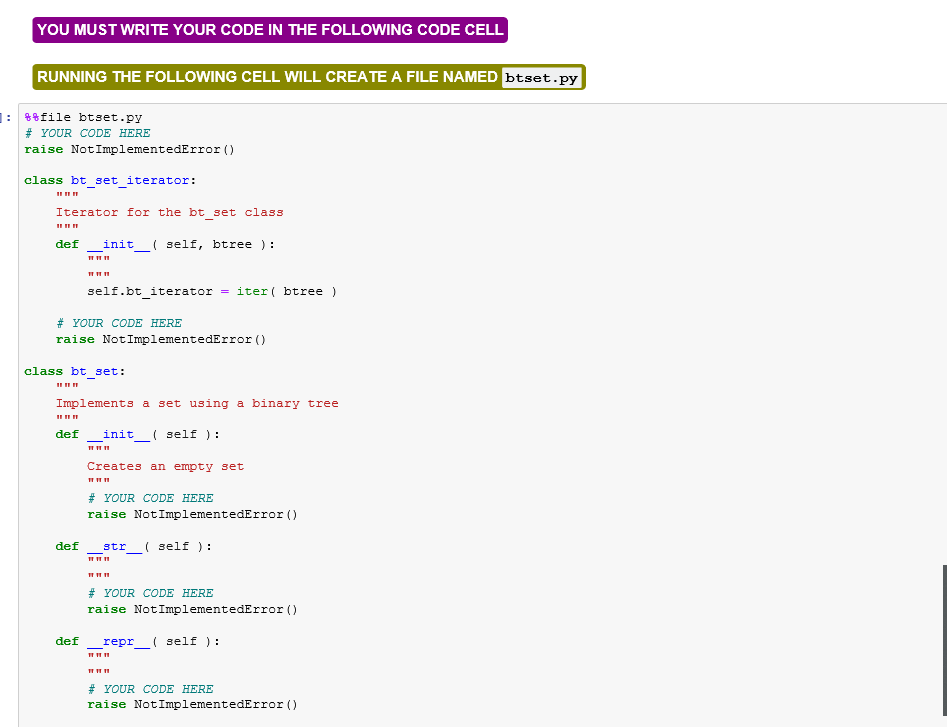



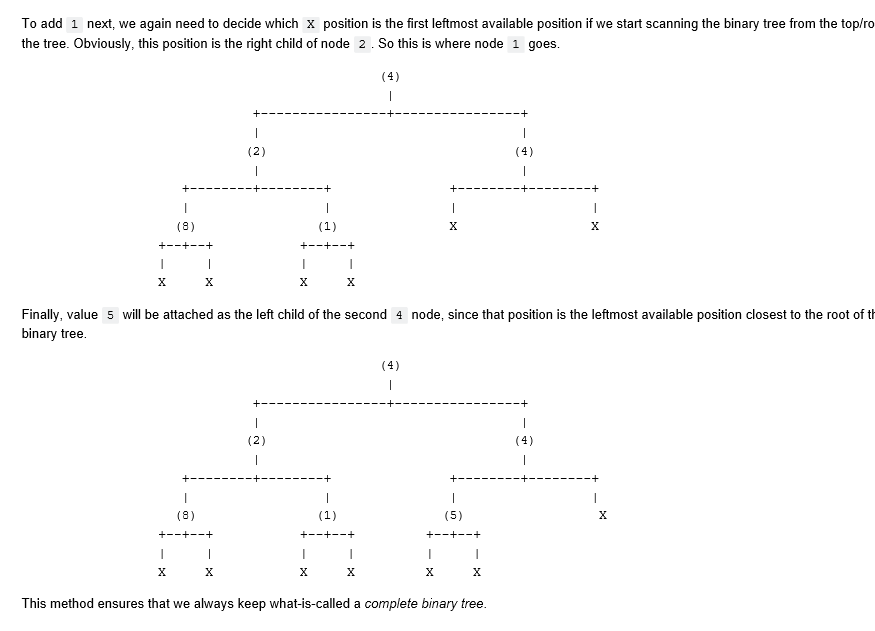
In this question, you will use your binary tree implementation from Quiz 5 to implement a set ADT. . First, you should have your binary_tree class implementation from Quiz 5 handy. You will have to copy and paste it into the code cell where you need to provide your complete solution for this question. . Second, implement a new class named bt_set that provides the following APls: 1. bt_set() must create and return an empty set. The items of the set must be stored in an instance variable named values , which must be of the binary_tree type. 2. bt_set.add( self, item ) must add the indicated (hashable) item to the set if that item is not already in the set. Otherwise, it should do nothing 3. bt_set. _iter_( self ) returns an iterator for the bt_set class instances. There is no particular traversal order required. This iterator must be implemented in a class named bt_set_iterator. See the incomplete implementation of this class provided for you below. 4. Your implementation should support the in operator so that x in s , where x is a value inserted into the bt_set instance, b, using bt_set.add() method returns True . Similarly, e in s should return False if element e is not in set, 3. 5. bt_set. _str_( self ) / bt_set. _repr__l self ) returns a string representation of the set enclosed in {...} in which individual items are separated by commas ( , ), as in the case of the Python set class. For example, if the bt_set instance, 3 , contains the items 5, 8, 4, and 9, then str( 3 ) should return {8, 4, 5, 9), where the order of items is immaterial. NOTE: No item removal method is required for this question! . You must implement your entire code without using any external libraries/modules. In other words, absolutely no import statements! This means that, as mentioned earlier, that you will have to copy and paste your binary_tree class implementation into the following code cell. . You cannot use the Python set class for any purpose whatsoever. Note that any deviation from any of these specifications will cost you points. Failure to abide by the strict programming rules mentioned here will result in zero grade automatically. For example, if you use even a single import statement in your code, you will get no grade for your work! YOU MUST WRITE YOUR CODE IN THE FOLLOWING CODE CELL RUNNING THE FOLLOWING CELL WILL CREATE A FILE NAMED btset.py #tfile btset.py # YOUR CODE HERE raise NotImplementedError() class bt_set_iterator: III Iterator for the bt_set class II III def init ( self, btree ) : self.bt_iterator = iter( btree ) # YOUR CODE HERE raise Not ImplementedError() class bt_set: Implements a set using a binary tree IT def init__(self): Creates an empty set # YOUR CODE HERE raise NotImplementedError() def str ( self ): # YOUR CODE HERE raise NotImplementedError() def repr (self): T1111 # YOUR CODE HERE raise NotImplementedError() def str (self): # YOUR CODE HERE raise NotImplementedError() def repr_(self): TTT 11 # YOUR CODE HERE raise NotImplementedError() def iter( self ): TTT! # YOUR CODE HERE raise NotImplementedError() def add( self, item ): TITI Adds the provided item if that item is not already in the set # YOUR CODE HERE raise NotImplementedError() In this question, you will implement a binary tree according to the following specifications: . Implement a Python class named binary_tree that provides the following APIs: 1. binary_tree () creates and returns an empty binary tree. Each node of the binary tree should be created as an instance of the bt_node class, whose (partial/incomplete) implementation has been provided to you below. The root of the binary must be stored in an instance variable named root. When the tree is empty, the root value must be None. In addition, the bt_node class must support the == operation. 2. binary_tree.insert( self, item ) should unconditionally insert the provided item in the binary tree. This function should insert the new item into the first leftmost position available that is closest to the root of tree. Hint: Consider using iteration/looping to implement this functionality! Example: Consider the following code snippet that adds some values to the binary tree, b b = binary_tree() for v in [4, 2, 4, 8, 1, 5]: # b.insert(v) Once the root node with value 4 is inserted into the binary tree, we have both of root's children empty. Empty child node positions will be indicated with x characters in the figures below. One node 4 becomes the root of the binary tree being built, we will have the following structure: (4) + -+ X Since we need to insert 2 next, we need to attach a new bt_node with value 2 as the left child of 4 , since that position is the first available leftmost position with respect to the root of the tree. So now the binary tree will look as follows: Since we need to insert 2 next, we need to attach a new bt_node with value 2 as the left child of 4 , since that position is the first available leftmost position with respect to the root of the tree. So now the binary tree will look as follows: (4) I + 1 1 (2) 1 +----+----+ 1 1 X To add the second 4 value, we need to determine to which x position this value will have to be attached according to the provided specifications. Going from the top to the bottom of the tree, the leftmost available position is the right child of the first 4 node. So we attach the second 4 there: (4) 1 1 (4) (2) +----+ +--- 1 1 xx The fourth value to be inserted into the binary tree is , and, obviously, the leftmost available position starting from the top of the tree is the left child of node 2 . So this is where & is attached. (4) 1 + + | (2) 1 | (4) 1 +- +- 1 (8) 1 X | X +--+--+ | X To add 1 next, we again need to decide which x position is the first leftmost available position if we start scanning the binary tree from the top/ro the tree. Obviously, this position is the right child of node 2. So this is where node 1 goes. + -+ | (2) (4) 1 | (8) X X +--+--+ 1 1 X X (1) +--+--+ 1 1 X Finally, value 5 will be attached as the left child of the second 4 node, since that position is the leftmost available position closest to the root of th binary tree. | + | (4) + + + + 1 1 (5) X 1 (8) +--+--+ I | X X 1 (1) +--+--+ 1 1 X +--+--+ I 1 X X This method ensures that we always keep what-is-called a complete binary tree. In this question, you will use your binary tree implementation from Quiz 5 to implement a set ADT. . First, you should have your binary_tree class implementation from Quiz 5 handy. You will have to copy and paste it into the code cell where you need to provide your complete solution for this question. . Second, implement a new class named bt_set that provides the following APls: 1. bt_set() must create and return an empty set. The items of the set must be stored in an instance variable named values , which must be of the binary_tree type. 2. bt_set.add( self, item ) must add the indicated (hashable) item to the set if that item is not already in the set. Otherwise, it should do nothing 3. bt_set. _iter_( self ) returns an iterator for the bt_set class instances. There is no particular traversal order required. This iterator must be implemented in a class named bt_set_iterator. See the incomplete implementation of this class provided for you below. 4. Your implementation should support the in operator so that x in s , where x is a value inserted into the bt_set instance, b, using bt_set.add() method returns True . Similarly, e in s should return False if element e is not in set, 3. 5. bt_set. _str_( self ) / bt_set. _repr__l self ) returns a string representation of the set enclosed in {...} in which individual items are separated by commas ( , ), as in the case of the Python set class. For example, if the bt_set instance, 3 , contains the items 5, 8, 4, and 9, then str( 3 ) should return {8, 4, 5, 9), where the order of items is immaterial. NOTE: No item removal method is required for this question! . You must implement your entire code without using any external libraries/modules. In other words, absolutely no import statements! This means that, as mentioned earlier, that you will have to copy and paste your binary_tree class implementation into the following code cell. . You cannot use the Python set class for any purpose whatsoever. Note that any deviation from any of these specifications will cost you points. Failure to abide by the strict programming rules mentioned here will result in zero grade automatically. For example, if you use even a single import statement in your code, you will get no grade for your work! YOU MUST WRITE YOUR CODE IN THE FOLLOWING CODE CELL RUNNING THE FOLLOWING CELL WILL CREATE A FILE NAMED btset.py #tfile btset.py # YOUR CODE HERE raise NotImplementedError() class bt_set_iterator: III Iterator for the bt_set class II III def init ( self, btree ) : self.bt_iterator = iter( btree ) # YOUR CODE HERE raise Not ImplementedError() class bt_set: Implements a set using a binary tree IT def init__(self): Creates an empty set # YOUR CODE HERE raise NotImplementedError() def str ( self ): # YOUR CODE HERE raise NotImplementedError() def repr (self): T1111 # YOUR CODE HERE raise NotImplementedError() def str (self): # YOUR CODE HERE raise NotImplementedError() def repr_(self): TTT 11 # YOUR CODE HERE raise NotImplementedError() def iter( self ): TTT! # YOUR CODE HERE raise NotImplementedError() def add( self, item ): TITI Adds the provided item if that item is not already in the set # YOUR CODE HERE raise NotImplementedError() In this question, you will implement a binary tree according to the following specifications: . Implement a Python class named binary_tree that provides the following APIs: 1. binary_tree () creates and returns an empty binary tree. Each node of the binary tree should be created as an instance of the bt_node class, whose (partial/incomplete) implementation has been provided to you below. The root of the binary must be stored in an instance variable named root. When the tree is empty, the root value must be None. In addition, the bt_node class must support the == operation. 2. binary_tree.insert( self, item ) should unconditionally insert the provided item in the binary tree. This function should insert the new item into the first leftmost position available that is closest to the root of tree. Hint: Consider using iteration/looping to implement this functionality! Example: Consider the following code snippet that adds some values to the binary tree, b b = binary_tree() for v in [4, 2, 4, 8, 1, 5]: # b.insert(v) Once the root node with value 4 is inserted into the binary tree, we have both of root's children empty. Empty child node positions will be indicated with x characters in the figures below. One node 4 becomes the root of the binary tree being built, we will have the following structure: (4) + -+ X Since we need to insert 2 next, we need to attach a new bt_node with value 2 as the left child of 4 , since that position is the first available leftmost position with respect to the root of the tree. So now the binary tree will look as follows: Since we need to insert 2 next, we need to attach a new bt_node with value 2 as the left child of 4 , since that position is the first available leftmost position with respect to the root of the tree. So now the binary tree will look as follows: (4) I + 1 1 (2) 1 +----+----+ 1 1 X To add the second 4 value, we need to determine to which x position this value will have to be attached according to the provided specifications. Going from the top to the bottom of the tree, the leftmost available position is the right child of the first 4 node. So we attach the second 4 there: (4) 1 1 (4) (2) +----+ +--- 1 1 xx The fourth value to be inserted into the binary tree is , and, obviously, the leftmost available position starting from the top of the tree is the left child of node 2 . So this is where & is attached. (4) 1 + + | (2) 1 | (4) 1 +- +- 1 (8) 1 X | X +--+--+ | X To add 1 next, we again need to decide which x position is the first leftmost available position if we start scanning the binary tree from the top/ro the tree. Obviously, this position is the right child of node 2. So this is where node 1 goes. + -+ | (2) (4) 1 | (8) X X +--+--+ 1 1 X X (1) +--+--+ 1 1 X Finally, value 5 will be attached as the left child of the second 4 node, since that position is the leftmost available position closest to the root of th binary tree. | + | (4) + + + + 1 1 (5) X 1 (8) +--+--+ I | X X 1 (1) +--+--+ 1 1 X +--+--+ I 1 X X This method ensures that we always keep what-is-called a complete binary tree
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


