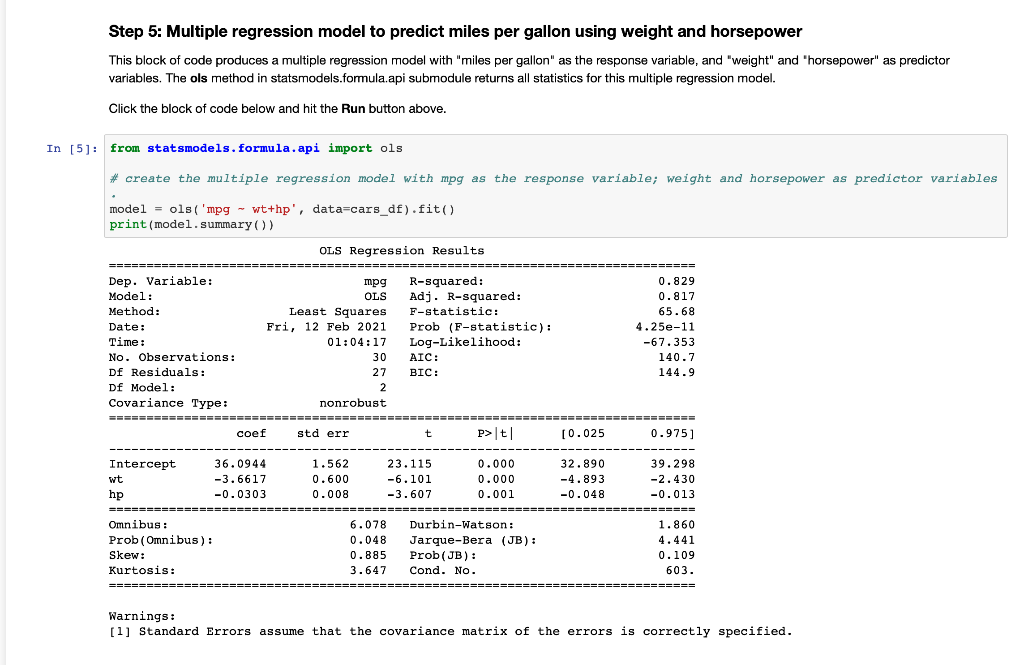
In your initial post, address the following items: 1. Is at least one of the two variables (weight and horsepower) significant in the model? Run the overall F-test and provide your interpretation at 5% level of significance. See Step 5 in the Python script. Include the following in your analysis: a. Define the null and alternative hypothesis in mathematical terms and in words. b. Report the level of significance. C. Include the test statistic and the P-value. (Hint: F-Statistic and Prob (F-Statistic) in the output). d. Provide your conclusion and interpretation of the test. Should the null hypothesis be rejected? Why or why not? 2. What is the slope coefficient for the weight variable? Is this coefficient significant at 5% level of significance (alpha=0.05)? (Hint: Check the P- value, P>|t|, for weight in Python output. Recall that this is the individual t- 2. What is the slope coefficient for the weight variable? Is this coefficient significant at 5% level of significance (alpha=0.05)? (Hint: Check the P- value, P>|t|, for weight in Python output. Recall that this is the individual t- test for the beta parameter.) See Step 5 in the Python script. 3. What is the slope coefficient for the horsepower variable? Is this coefficient significant at 5% level of significance (alpha=0.05)? (Hint: Check the P- value, P>[t], for horsepower in Python output. Recall that this is the individual t-test for the beta parameter.) See Step 5 in the Python script. 4. What is the purpose of performing individual t-tests after carrying out the overall F-test? What are the differences in the interpretation of the two tests? 5. What is the coefficient of determination of your multiple regression model from Module Six? Provide appropriate interpretation of this statistic. Step 5: Multiple regression model to predict miles per gallon using weight and horsepower This block of code produces a multiple regression model with "miles per gallon" as the response variable, and "weight" and "horsepower" as predictor variables. The ols method in statsmodels.formula.api submodule returns all statistics for this multiple regression model. Click the block of code below and hit the Run button above. In [5]: from statsmodels. formula.api import ols # create the multiple regression model with mpg as the response variable; weight and horsepower as predictor variables ====== model = ols('mpg - wt+hp', data=cars_df).fit() print(model.summary()) OLS Regression Results ================ Dep. Variable: mpg R-squared: Model: OLS Adj. R-squared: Method: Least Squares F-statistic: Date: Fri, 12 Feb 2021 Prob (F-statistic): Time: 01:04:17 Log-Likelihood: No. Observations: 30 AIC: Df Residuals: 27 BIC: Df Model: 2 Covariance Type: nonrobust =========== coef std err t P>t 0.829 0.817 65.68 4.25e-11 -67.353 140.7 144.9 ===== [0.025 0.975] Intercept wt hp 36.0944 -3.6617 -0.0303 32.890 -4.893 -0.048 39.298 -2.430 -0.013 ==== Omnibus: Prob (Omnibus) : Skew: Kurtosis: 1.562 23.115 0.000 0.600 -6.101 0.000 0.008 -3.607 0.001 ===== ======= 6.078 Durbin-Watson: 0.048 Jarque-Bera (JB): 0.885 Prob(JB): 3.647 Cond. No. 1.860 4.441 0.109 603. Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified