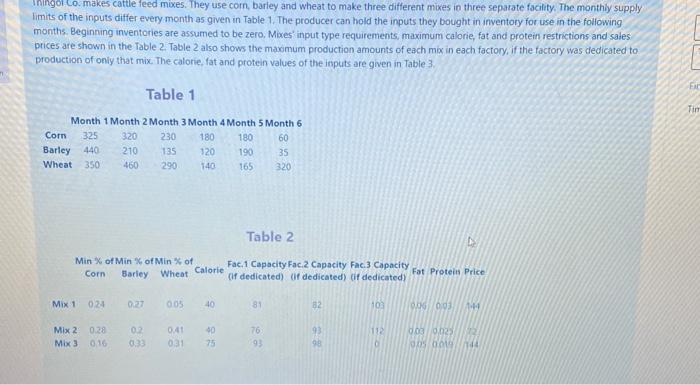
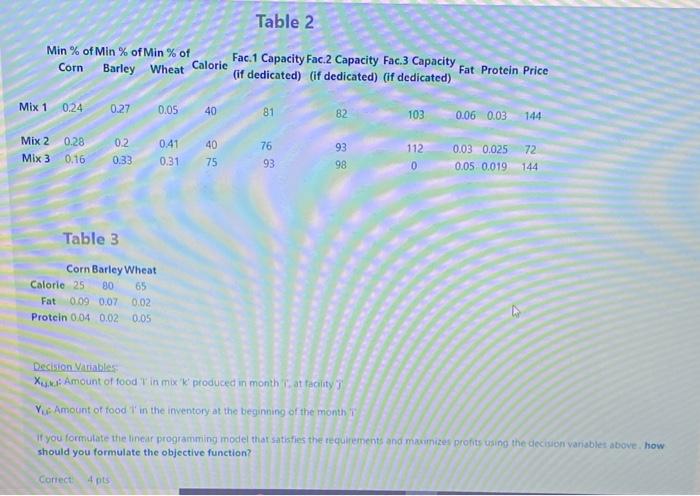
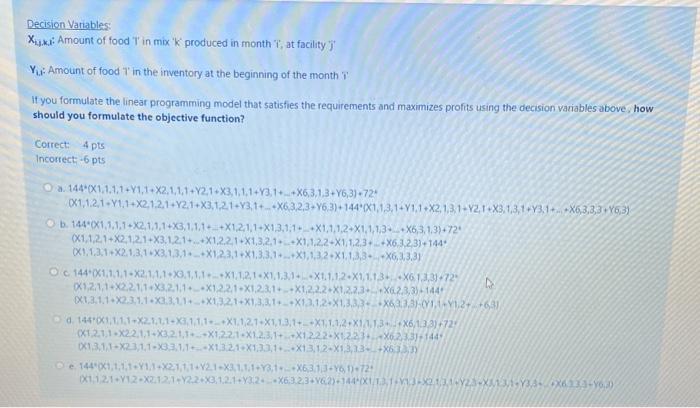
Iningol Lo makes cattle feed mixes. They use com, barley and wheat to make three different mixes in three separate facility. The monthly supply limits of the inputs differ every month as given in Table 1. The producer can hold the inputs they bought in inventory for use in the following months Beginning inventories are assumed to be zero. Mixes input type requirements, maximum calorie, fat and protein restrictions and sales prices are shown in the Table 2. Table 2 also shows the maximum production amounts of each mix in each factory, if the factory was dedicated to production of only that mix. The calorie, fat and protein values of the inputs are given in Table 3 FC Table 1 Tin Month 1 Month 2 Month 3 Month 4 Month 5 Month 6 Com 325 320 230 180 180 60 Barley 440 210 135 320 190 35 Wheat 460 290 140 165 320 350 Table 2 24 Min X of Min of Min % of Fac. 1 Capacity Fac.2 Capacity Fac.3 Capacity Corn Calorie Barley Wheat of dedicated) Of dedicated) Oif dedicated Fat Protein Price Mix 1 024 0.27 005 40 81 82 103 0.06 0.03 Mix 2 0.41 93 112 0.28 0.16 02 033 40 75 76 9 002 0000 Mix 3 021 T Table 2 Min % of Min % of Min % of Fac.1 Capacity Fac.2 Capacity Fac.3 Capacity Corn Barley Wheat Calorie Fat Protein Price (if dedicated) (if dedicated) of dedicated) Mix 10.24 0.27 0.05 40 81 82 103 0.06 0.03 144 0.2 0.41 40 Mix 2 0.28 Mix 3 0.16 76 93 112 72 0.33 0.31 75 93 98 0.03 0.025 0.05 0.019 0 144 Table 3 Corn Barley Wheat Calorie 25 30 65 Fat 0.09 0.07 0.02 Protein 0.04 0.02 0.05 Decision Variables Xxx Amount of food in mix k produced in month at facility V Amount of food in the inventory at the beginning of the month if you formulate the linear programming model that satisfies the requirements and maizes profits using the decision variablet above how should you formulate the objective function? correct 4 pts Decision Variables Xux: Amount of food in mix 'k produced in month 1, at facility Yu: Amount of food in the inventory at the beginning of the month If you formulate the linear programming model that satisfies the requirements and maximizes profits using the decision variables above how should you formulate the objective function? Correct 4 pts Incorrect 6 pts a 1440X1.1.1.1.1.1-X2,1,1.1.2.1.3.1.1.1.3.1++X6,3,1,3 +Y6,3)+72 0x1,12,1.1.1+X2.1.2.1.2.1.3.1.2 1+Y3,1++X632,3 -76,3)+1440x1,1,3,1-11-X2,131-Y21X3,1,3,1.3.1+ X6,3,3,3*Y63) b. 144"X1.1.1.1.2.1.1.1 X3.1.1.1++X1,2 1,1-X1,3,1.1..X1,1,1,2-X1,1,1,3 X63 1.3)+72 (X1.1.2.1.2.1.2.1-X3.1.2.1X12.21*X1,3,2,1...+X1.1.2.2-X1.123X6.32,3)+144 X1.1.3.1.X2.1.3.1.3.1.3.1._+X123,1X1,33.1...+X1.1.3.2-X11.33 X6,3.3.3 144X1,1.1.1.2.1.1.1 X3.1.1.1:+X1.1.2.1-X1,13,14X1.1.1.2-X1,1.1.3.X6133-72 X12.1.1.X221.1.3.2.1.1. X12.2.1 X1 2.3.1++X1,2,22-X12.73*X62,3,3). 144 X1.3.1.1.x2.3.1.1-x2.3.1.1.X1.3.2.1+x13.3.1++X12.1.2-X1,333.X6333-011-912-631 d. 1440x1,1.1.1-2.1.1.1-1.1.1.10X1.1.2.1-X1,1.3.1+ --X11.1.2-X1/13*X61.33)+727 X1 2.1.1.x22.1.1-X3.2.1.1.X1,22.1.1.2.3.1+ X1222-X122X62,3144 13.1.1-x23,1.1.3.1.1-1.3 2.1X1231X1312-X13,13+X51 e. 144x1.1.1.1.91.1 X2.11 1.2.1-3.1.1.1+Y3.1.X633-761)-724 X1121+Y12-X2.12.1-Y22-23.1.2.1.3.2.X63.23762-14XLT 3X2X1Y3X6233-2)