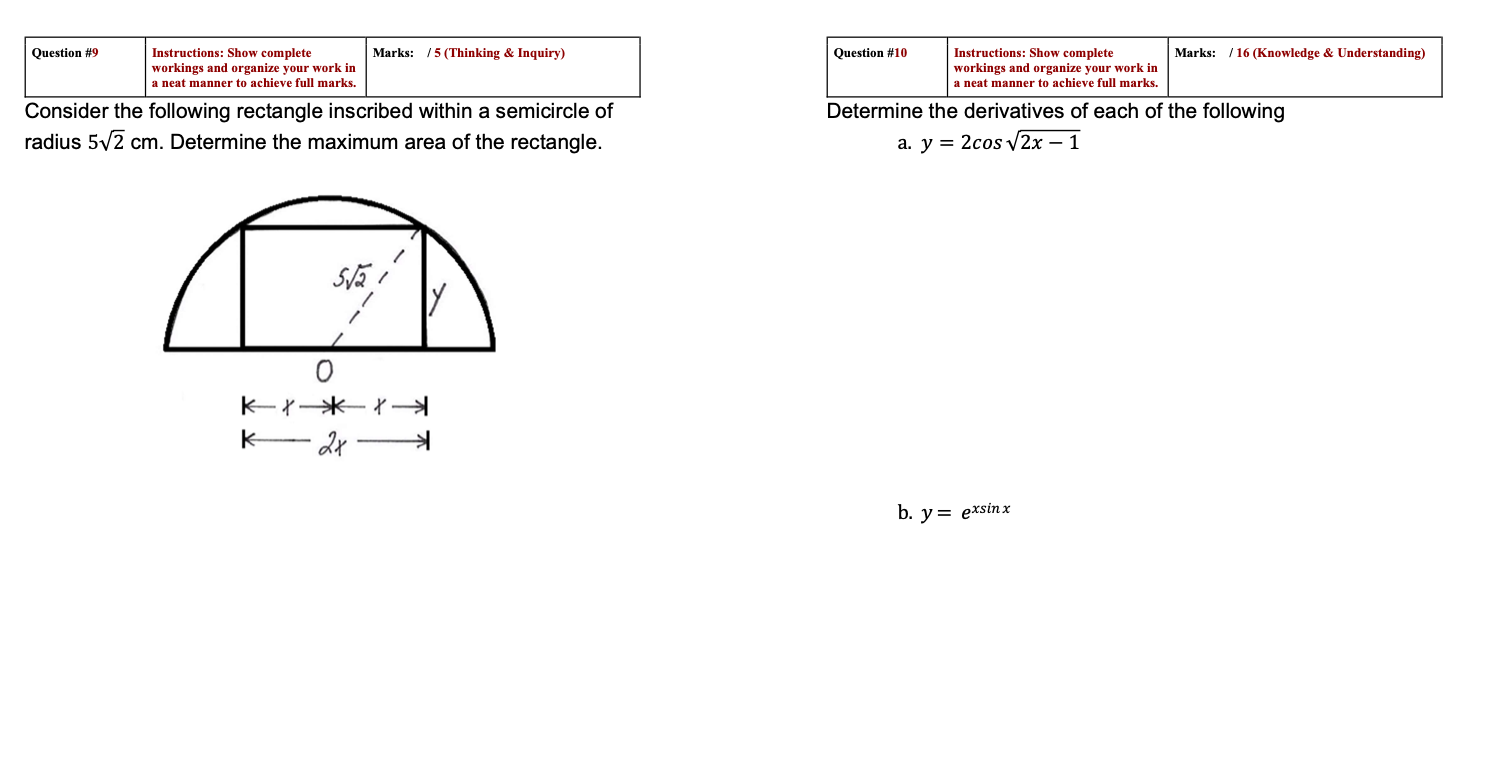
Instructions: Show complete Marks: 1'5 (Thinking 8: Inquiry) Question it'll] Instructions: Show complete Marks: 1' 16 (Knowledge n Understanding) working: and organize your work in working: and arguing your work in a neat mannerto achieve full marks. a neat manner to achieve full marks. Considerthe following rectangle inscribed within a semicircle of Determine the derivatives of each of the following radius 5J5 cm. Determine the maximum area of the rectangle. a. y = Econ/2x 1 b. y: exsinx Question #2 Instructions: Show complete Marks: /5 (Application) Question #3 Instructions: Show complete Marks: /5 (Application) workings and organize your work in /2 (Communication) workings and organize your work in /2 (Communication) a neat manner to achieve full marks. a neat manner to achieve full marks. Determine the equation of the tangent to the curve Determine the value(s) at which the function y = (3x3 + 5)(x -7)2 y = -2x3 - 5x2 at the point where x = 3. has a tangent with a slope of -4.Question #6 Instructions: Show complete Marks: /8 (Knowledge & Understanding) Question #7 Instructions: Show complete Marks: /5 (Application) workings and organize your work in workings and organize your work in /3 (Communication) a neat manner to achieve full marks. a neat manner to achieve full marks. Consider the following functions and state the equations of any Determine the critical points of the following function and classify and all asymptotes them as local minima or local maxima using the second derivative a. f(x) = 3x2+7 test f (x) = x2e-x x2 +x-6 b. f(x) = -3x2+2 x-1c. y = exsin 3x Question #11 Instructions: Show complete Marks: /5 (Application) workings and organize your work in /2 (Communication) a neat manner to achieve full marks. Determine the equation of the normal line to the curve y = xVx2 - 3 at x = 2. d. y = (x - 3)(e3x)Section: A Knowledge Communication Thinking Application b. f (x ) = x4 - 2x3+ 1 & & Understanding Inquiry CALCULUS 155 / 17 / 30 Question #1 Instructions: Show complete Marks: / 16 (Knowledge & Understanding) workings and organize your work in a neat manner to achieve full marks. Determine the derivative of each of the following functions. a. f (t) = (2+2 + vt ) (6t - 1) c. f(x) = (6x + 5)(4x - 1) d. f (x) =4 3x x+ + 6 V xQuestion H8 Instruction: Show complete Marks: 1' HI (Application) workings and organize your work in M (Communication) a neat manner to achieve full marks. Perform a thorough analysis using the algorithm for curve sketching of the following function. x2+I+2 \"xi-T That is to say, identify all asymptotes, intercepts, restrictions, critical points, inflection points, and several other key points to construct an accurate graph of the function. Show all your workings for full marks. Graph paper is provided on the following page