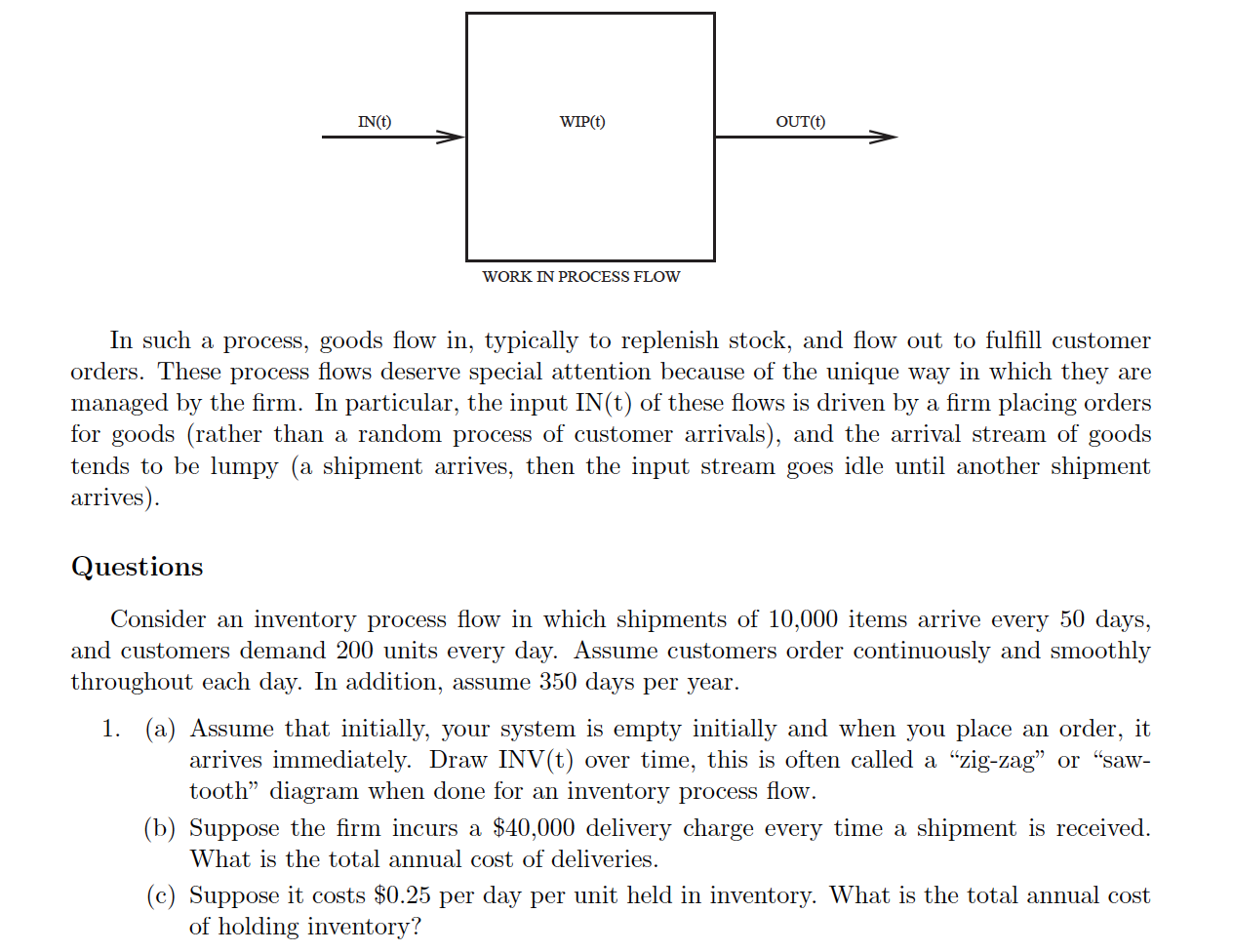
IN(t) WIP(t) OUT(t) WORK IN PROCESS FLOW In such a process, goods flow in, typically to replenish stock, and flow out to fulfill customer orders. These process flows deserve special attention because of the unique way in which they are managed by the firm. In particular, the input IN(t) of these flows is driven by a firm placing orders for goods (rather than a random process of customer arrivals), and the arrival stream of goods tends to be lumpy (a shipment arrives, then the input stream goes idle until another shipment arrives) Questions Consider an inventory process flow in which shipments of 10,000 items arrive every 50 days, and customers demand 200 units every day. Assume customers order continuously and smoothly throughout each day. In addition, assume 350 days per year. 1. (a) Assume that initially, your system is empty initially and when you place an order, it arrives immediately. Draw INV(t) over time, this is often called a "zig-zag" or "saw- tooth diagram when done for an inventory process flow. (b) Suppose the firm incurs a $40,000 delivery charge every time a shipment is received. What is the total annual cost of deliveries. (c) Suppose it costs $0.25 per day per unit held in inventory. What is the total annual cost of holding inventory? 2. Now suppose that the firm decides to order shipments of size 7,000 items that will arrive at regular intervals. (a) Assume again that your system is empty initially. How often should the orders arrive? (b) Draw INV(t) over time under this new ordering policy. (c) What is the new total annual cost of deliveries. (d) What is the new total annual cost of holding inventory? 3. What order quantity do you recommend to minimize their combined annual ordering and inventory-holding costs? IN(t) WIP(t) OUT(t) WORK IN PROCESS FLOW In such a process, goods flow in, typically to replenish stock, and flow out to fulfill customer orders. These process flows deserve special attention because of the unique way in which they are managed by the firm. In particular, the input IN(t) of these flows is driven by a firm placing orders for goods (rather than a random process of customer arrivals), and the arrival stream of goods tends to be lumpy (a shipment arrives, then the input stream goes idle until another shipment arrives) Questions Consider an inventory process flow in which shipments of 10,000 items arrive every 50 days, and customers demand 200 units every day. Assume customers order continuously and smoothly throughout each day. In addition, assume 350 days per year. 1. (a) Assume that initially, your system is empty initially and when you place an order, it arrives immediately. Draw INV(t) over time, this is often called a "zig-zag" or "saw- tooth diagram when done for an inventory process flow. (b) Suppose the firm incurs a $40,000 delivery charge every time a shipment is received. What is the total annual cost of deliveries. (c) Suppose it costs $0.25 per day per unit held in inventory. What is the total annual cost of holding inventory? 2. Now suppose that the firm decides to order shipments of size 7,000 items that will arrive at regular intervals. (a) Assume again that your system is empty initially. How often should the orders arrive? (b) Draw INV(t) over time under this new ordering policy. (c) What is the new total annual cost of deliveries. (d) What is the new total annual cost of holding inventory? 3. What order quantity do you recommend to minimize their combined annual ordering and inventory-holding costs