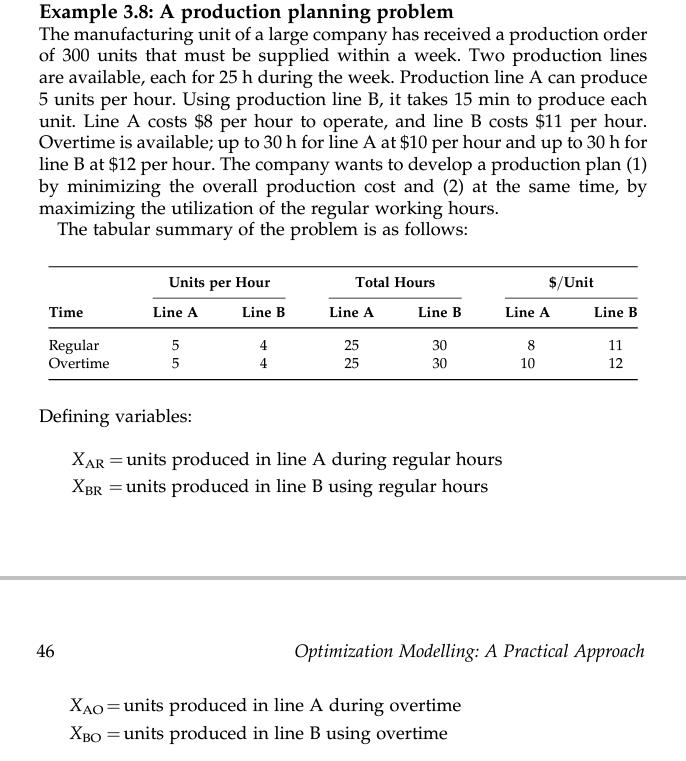
Integer programming (IP) is an extension of the general linear programming problem. The decision variables of an optimal solution to a general linear programming problem may take on either nonnegative fractional values or integer values. Unfortunately, fractional values are neither practical nor very meaningful in certain types of business, manufacturing, or defense problems. For example, two-thirds of a tank or half an aircraft cannot be bought or used in reality. One can assume integer programming as being a linear program with indivisibility requirements. There are three types of integer programming models: Integer: Where all the decision variables are integers. Binary integer: Where all the decision variable values are binary (either zero or one) only. There are some situations, where vari- ables can assume only one of two values (e.g., yes or no) that can be designated as zero and one. Mixed integer or mixed integer linear: Linear programs with some integer and some real decision variables. Example 3.8: A production planning problem The manufacturing unit of a large company has received a production order of 300 units that must be supplied within a week. Two production lines are available, each for 25 h during the week. Production line A can produce 5 units per hour. Using production line B, it takes 15 min to produce each unit. Line A costs $8 per hour to operate, and line B costs $11 per hour. Overtime is available; up to 30 h for line A at $10 per hour and up to 30 h for line B at $12 per hour. The company wants to develop a production plan (1) by minimizing the overall production cost and (2) at the same time, by maximizing the utilization of the regular working hours. The tabular summary of the problem is as follows: Time Regular Overtime Units per Hour 46 Line A 5 5 Line B 4 4 Total Hours Line A 25 25 Line B 30 30 Defining variables: XAR = units produced in line A during regular hours XBR = units produced in line B using regular hours XAO = units produced in line A during overtime XBO = units produced in line B using overtime $/Unit Line A 8 10 Line B 11 12 Optimization Modelling: A Practical Approach