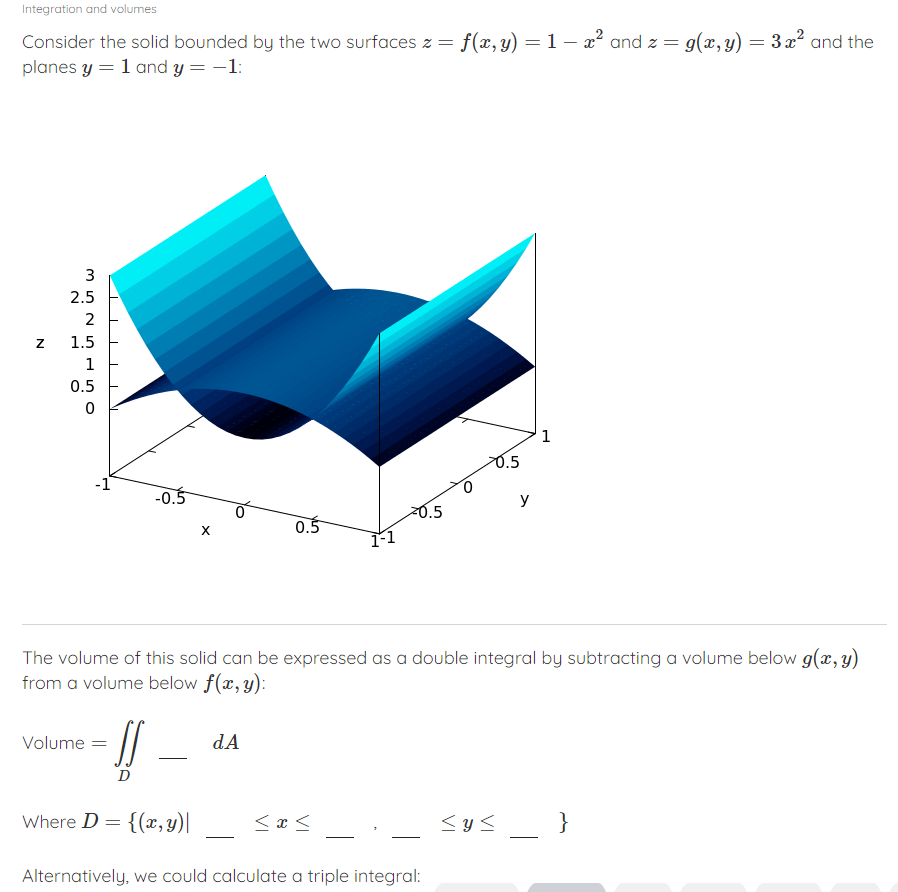
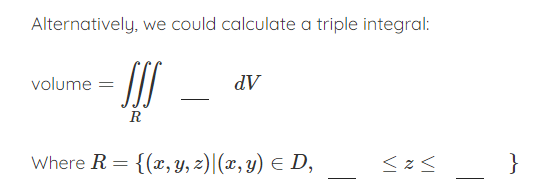
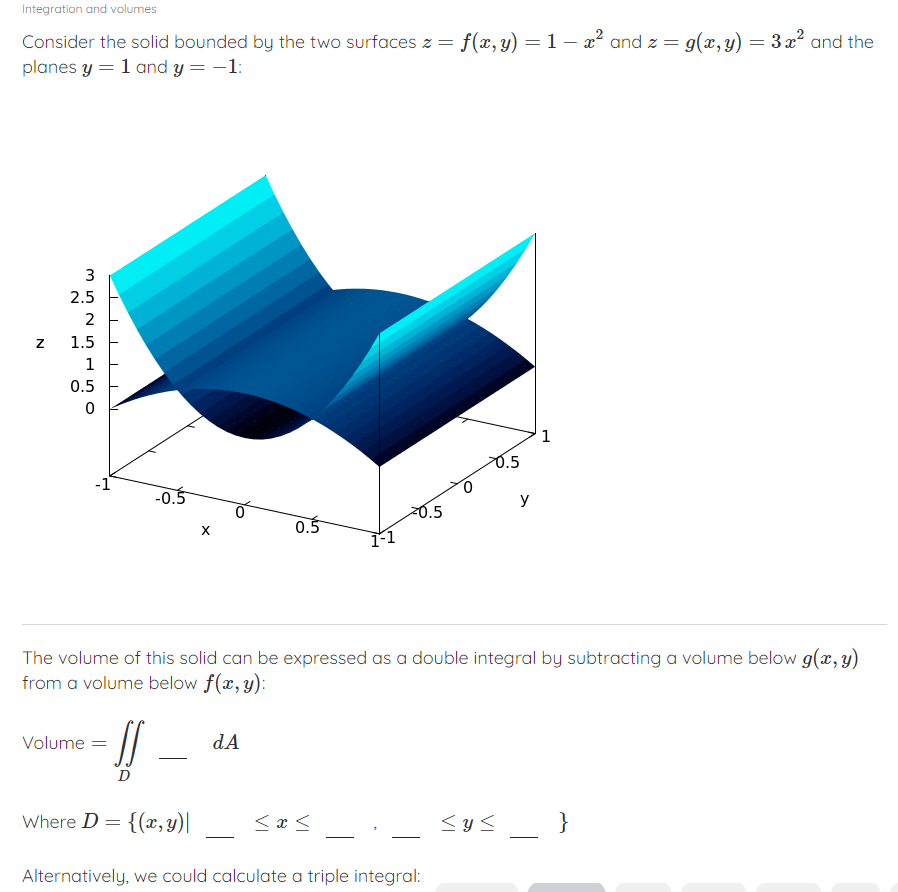
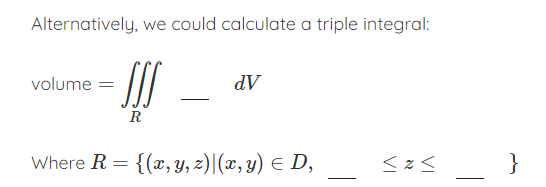
Integration and volumes Consider the solid bounded by the two surfaces z = f(x, y) = 1 - x and z = g(x, y) = 3x and the planes y = 1 and y = -1: N OUHU NOW Z -0.5 -0.5 y 0 -0.5 X 0.5 1-1 The volume of this solid can be expressed as a double integral by subtracting a volume below g(x, y) from a volume below f(x, y): Volume = - dA D Where D = {(x, y)| Alternatively, we could calculate a triple integral:Alternatively, we could calculate a triple integral: volume = dV R Where R = {(x, y, 2)|(x, y) ED