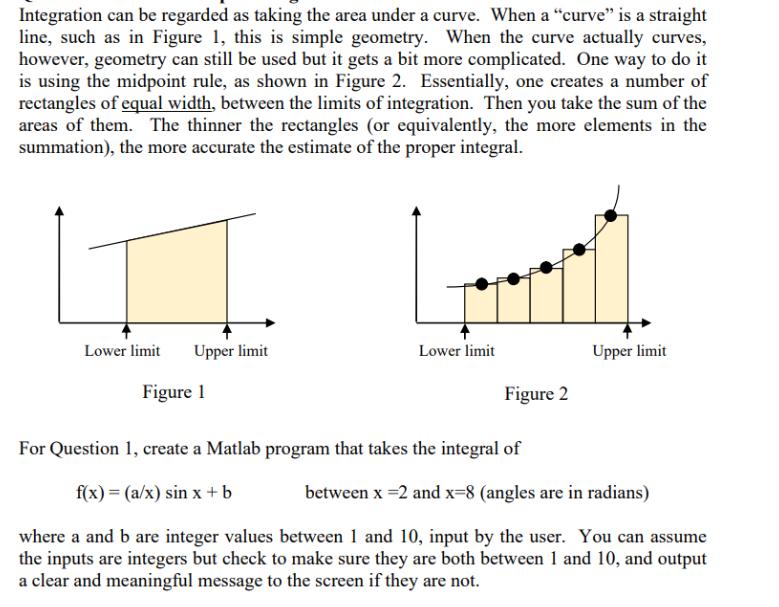
Integration can be regarded as taking the area under a curve. When a "curve" is a straight line, such as in Figure 1, this is simple geometry. When the curve actually curves, however, geometry can still be used but it gets a bit more complicated. One way to do it is using the midpoint rule, as shown in Figure 2. Essentially, one creates a number of rectangles of equal width, between the limits of integration. Then you take the sum of the areas of them. The thinner the rectangles (or equivalently, the more elements in the summation), the more accurate the estimate of the proper integral. Lower limit Upper limit Figure 1 Lower limit Upper limit Figure 2 For Question 1, create a Matlab program that takes the integral of f(x) (a/x) sin x+b between x =2 and x=8 (angles are in radians) where a and b are integer values between 1 and 10, input by the user. You can assume the inputs are integers but check to make sure they are both between 1 and 10, and output a clear and meaningful message to the screen if they are not.