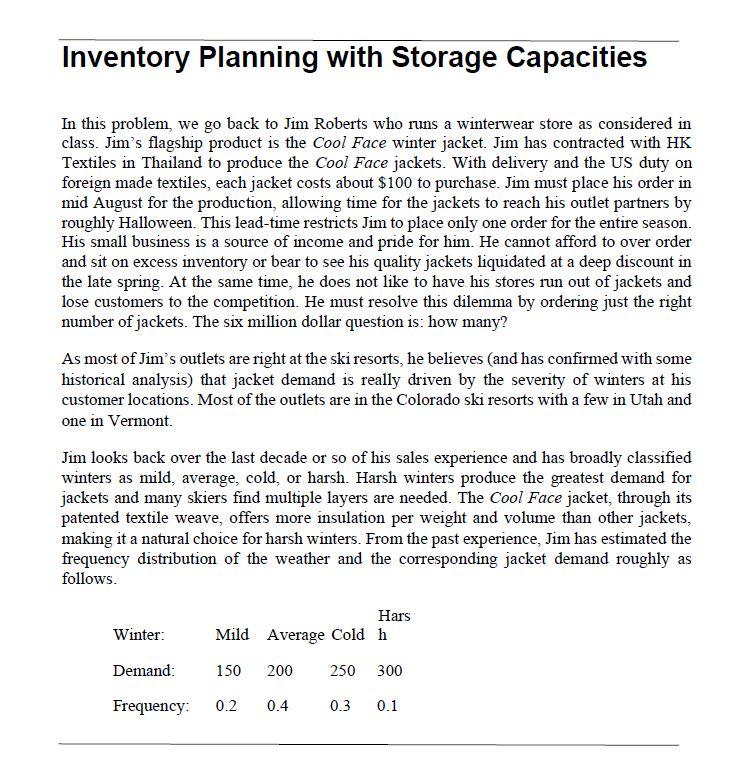
Inventory Planning with Storage Capacities In this problem, we go back to Jim Roberts who runs a winterwear store as considered in class. Jim's flagship product is the Cool Face winter jacket. Jim has contracted with HK Textiles in Thailand to produce the Cool Face jackets. With delivery and the US duty on foreign made textiles, each jacket costs about $100 to purchase. Jim must place his order in mid August for the production, allowing time for the jackets to reach his outlet partners by roughly Halloween. This lead-time restricts Jim to place only one order for the entire season. His small business is a source of income and pride for him. He cannot afford to over order and sit on excess inventory or bear to see his quality jackets liquidated at a deep discount in the late spring. At the same time, he does not like to have his stores run out of jackets and lose customers to the competition. He must resolve this dilemma by ordering just the right number of jackets. The six million dollar question is: how many? As most of Jim's outlets are right at the ski resorts, he believes (and has confirmed with some historical analysis) that jacket demand is really driven by the severity of winters at his customer locations. Most of the outlets are in the Colorado ski resorts with a few in Utah and one in Vermont Jim looks back over the last decade or so of his sales experience and has broadly classified winters as mild, average, cold, or harsh. Harsh winters produce the greatest demand for jackets and many skiers find multiple layers are needed. The Cool Face jacket, through its patented textile weave, offers more insulation per weight and volume than other jackets, making it a natural choice for harsh winters. From the past experience, Jim has estimated the frequency distribution of the weather and the corresponding jacket demand roughly as follows. Winter: Hars Mild Average Cold h 150 200 250 300 Demand: Frequency: 0.2 0.4 0.3 0.1 Jim sells jackets to the shops for $250 each, with most stores marking them up another $100 or so. If the actual demand exceeds the stock on hand, the Jim loses profit on the forgone sales. This often is an unpleasant situation as he gets calls from the Ski shops wanting more jackets, yet he can only promise them the next year around. On the other hand, in case of a shortfall in demand, the ski shops return any leftover jackets to Jim who then has to sell them at a discount outlet for $50 a piece at the end of the season, leaving him with a $50 loss. In the class, we considered this problem and solved it for Jim using simulation optimization. We now have a different situation. Jim is expanding his collection to hats and shoes. The demand for both these items also varies with winter in the following manner. Winter: Hars Mild Average Cold h Hats: 250 325 600 300 Shoes: 150 175 200 225 Frequency: 0.2 0.4 0.3 0.1 With additional item types. Jim also has to worry about his store capacity. His store has a total storage capacity of 200 cu A. The buying price, selling price, salvage price and the storage volumes are given in the table. Storagevol Item Buying Price Selling Price SalvagePrice (cu.ft.) Jackets 100 250 0.5 Shoes 60 100 Hats 30 80 20 0.1 50 30 0.2 Given the space considerations, profit margins, and demand uncertainty, how many of each item should Jim order? Use simulation (as in the class) simulate future scenarios of the demand and use optimization with space constraints to determine how many of each item to order. Please attach the excel sheet and a report detailing your approach. Inventory Planning with Storage Capacities In this problem, we go back to Jim Roberts who runs a winterwear store as considered in class. Jim's flagship product is the Cool Face winter jacket. Jim has contracted with HK Textiles in Thailand to produce the Cool Face jackets. With delivery and the US duty on foreign made textiles, each jacket costs about $100 to purchase. Jim must place his order in mid August for the production, allowing time for the jackets to reach his outlet partners by roughly Halloween. This lead-time restricts Jim to place only one order for the entire season. His small business is a source of income and pride for him. He cannot afford to over order and sit on excess inventory or bear to see his quality jackets liquidated at a deep discount in the late spring. At the same time, he does not like to have his stores run out of jackets and lose customers to the competition. He must resolve this dilemma by ordering just the right number of jackets. The six million dollar question is: how many? As most of Jim's outlets are right at the ski resorts, he believes (and has confirmed with some historical analysis) that jacket demand is really driven by the severity of winters at his customer locations. Most of the outlets are in the Colorado ski resorts with a few in Utah and one in Vermont Jim looks back over the last decade or so of his sales experience and has broadly classified winters as mild, average, cold, or harsh. Harsh winters produce the greatest demand for jackets and many skiers find multiple layers are needed. The Cool Face jacket, through its patented textile weave, offers more insulation per weight and volume than other jackets, making it a natural choice for harsh winters. From the past experience, Jim has estimated the frequency distribution of the weather and the corresponding jacket demand roughly as follows. Winter: Hars Mild Average Cold h 150 200 250 300 Demand: Frequency: 0.2 0.4 0.3 0.1 Jim sells jackets to the shops for $250 each, with most stores marking them up another $100 or so. If the actual demand exceeds the stock on hand, the Jim loses profit on the forgone sales. This often is an unpleasant situation as he gets calls from the Ski shops wanting more jackets, yet he can only promise them the next year around. On the other hand, in case of a shortfall in demand, the ski shops return any leftover jackets to Jim who then has to sell them at a discount outlet for $50 a piece at the end of the season, leaving him with a $50 loss. In the class, we considered this problem and solved it for Jim using simulation optimization. We now have a different situation. Jim is expanding his collection to hats and shoes. The demand for both these items also varies with winter in the following manner. Winter: Hars Mild Average Cold h Hats: 250 325 600 300 Shoes: 150 175 200 225 Frequency: 0.2 0.4 0.3 0.1 With additional item types. Jim also has to worry about his store capacity. His store has a total storage capacity of 200 cu A. The buying price, selling price, salvage price and the storage volumes are given in the table. Storagevol Item Buying Price Selling Price SalvagePrice (cu.ft.) Jackets 100 250 0.5 Shoes 60 100 Hats 30 80 20 0.1 50 30 0.2 Given the space considerations, profit margins, and demand uncertainty, how many of each item should Jim order? Use simulation (as in the class) simulate future scenarios of the demand and use optimization with space constraints to determine how many of each item to order. Please attach the excel sheet and a report detailing your approach