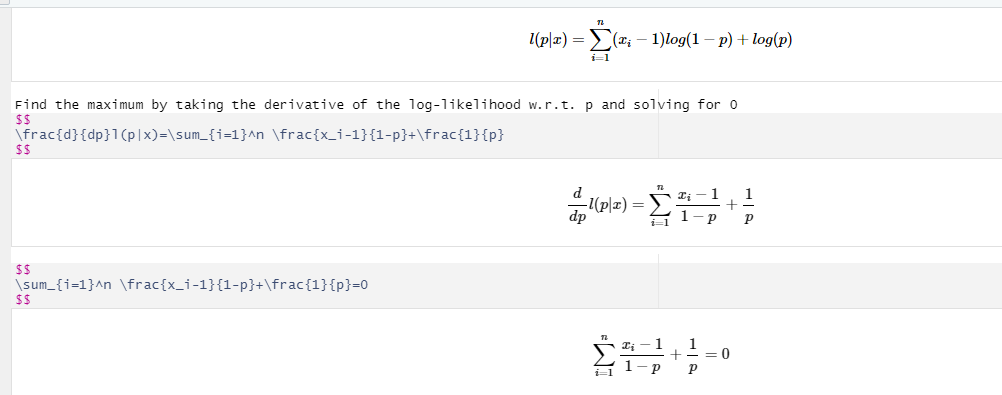
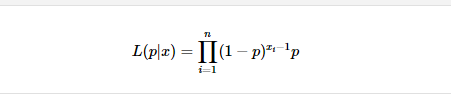
I(plz) = (x; - 1)log(1 - P) + log(p) i-1 Find the maximum by taking the derivative of the log-likelihood w.r. t. p and solving for 0 $$ \\frac{d} {dp}1(p|x)=\\sum_{i=1}An \\frac{x_i-1}{1-p}+\\frac{1}{p} d 1(plz)= Ci - 1 + dp 1 - p $5 \\sum_{i=1}An \\frac{x_i-1}{1-p}+\\frac{1}{p}=0 $5 Ci 1 = 0 1 -P