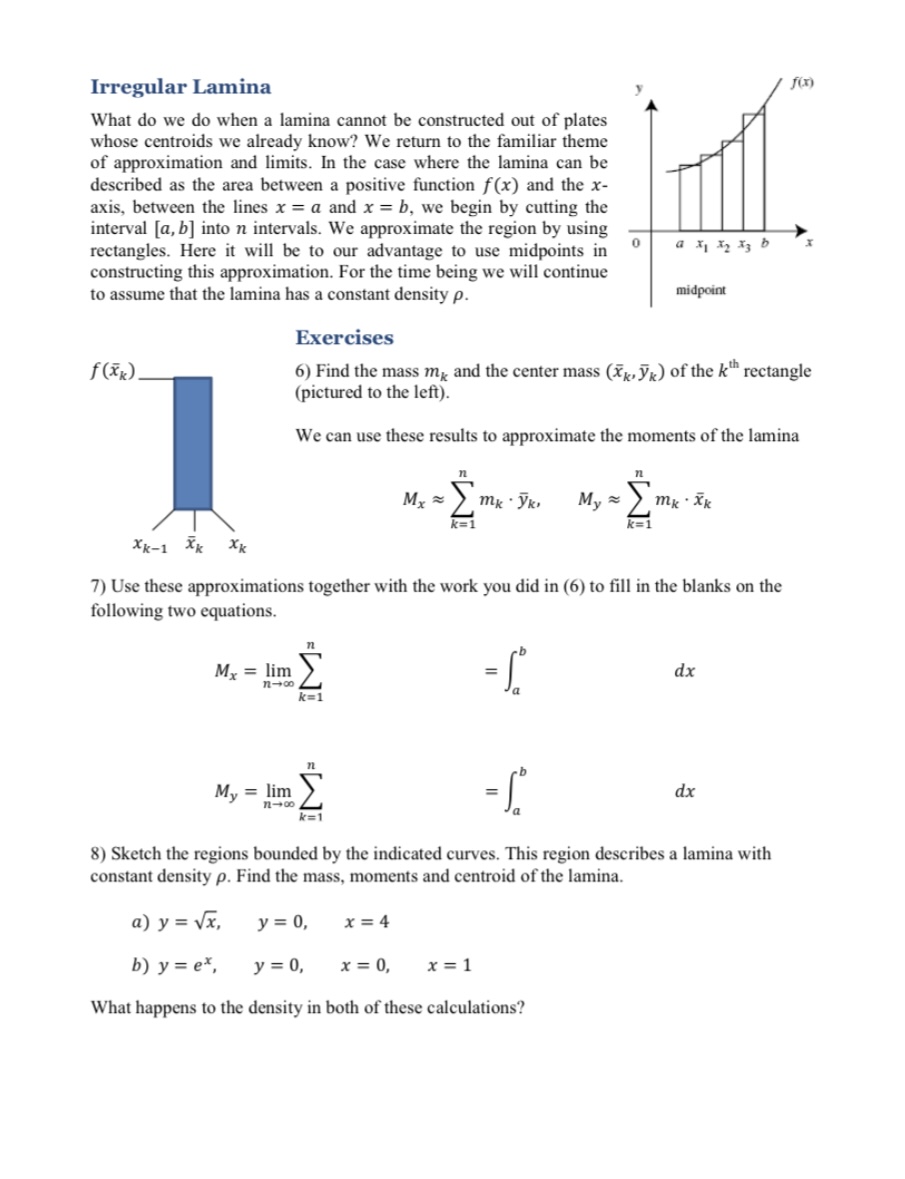
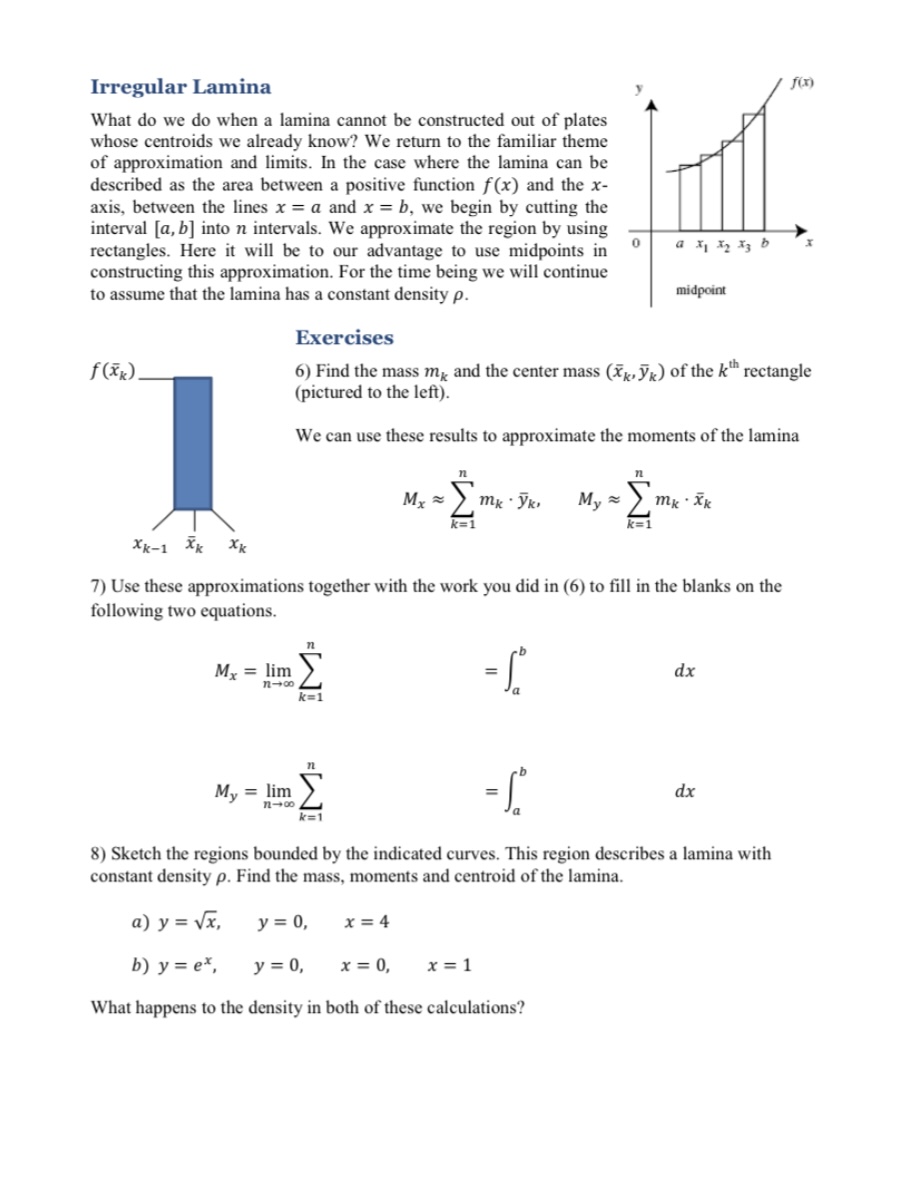
Irregular Lamina What do we do when a lamina cannot be constructed out of plates whose centroids we already know? We return to the familiar theme of approximation and limits. In the case where the lamina can be described as the area between a positive function f(x) and the x- axis, between the lines x = a and x = b, we begin by cutting the interval [a, b] into n intervals. We approximate the region by using rectangles. Here it will be to our advantage to use midpoints in a x Xy X3 b constructing this approximation. For the time being we will continue to assume that the lamina has a constant density p. midpoint Exercises f(Xx ) 6) Find the mass m, and the center mass (Xk. Vk) of the k rectangle (pictured to the left). We can use these results to approximate the moments of the lamina My = mk . VK. My = k=1 Xk-1 Xk XK 7) Use these approximations together with the work you did in (6) to fill in the blanks on the following two equations. Mx = lim M dx n-+co My = lim IM= n-+00 - 1 dx 8) Sketch the regions bounded by the indicated curves. This region describes a lamina with constant density p. Find the mass, moments and centroid of the lamina. a) y = vx, y=0, x= 4 b) y = ex, y= 0, x = 0, x =1 What happens to the density in both of these calculations