is one problem. differential equation.

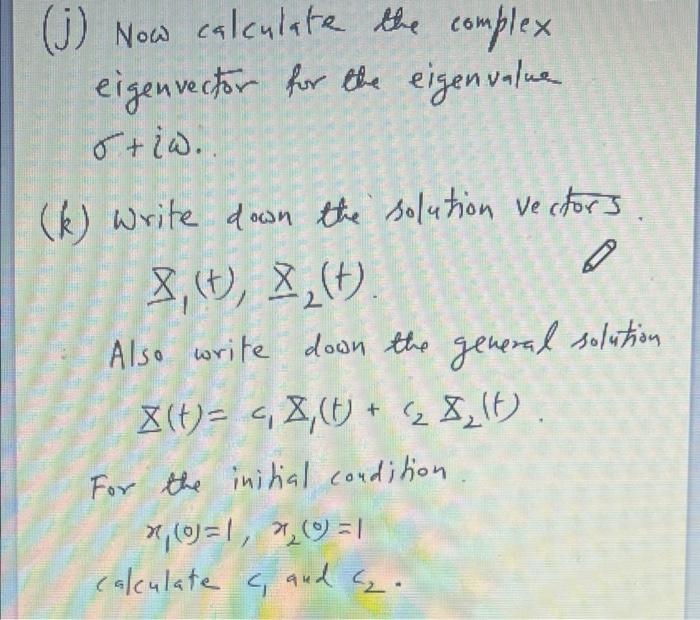
(B) we now add friction to our pendulum equation. The new equation is ** 2 x = x2 x = -12 sinx, -22. (h) Linearize 1 using Taylor's expansion in the vicinity of x= x=0, and , - write down M. X = MX stiw (i) Calculate the two complex eigenvalues of M. What are 6 and w for this problem. (j) Now calculate the complex eigenvector for the eigenvalue &tiw. (k) write down the solution vectors 3,(), , (+) Also write down the general solution X(t)= 4,8,0) + (2 8,10 For the initial condition X, (0:1, 2,0:1 calculates, and a + (1) Ignoring the pot { term as in Be define it, tits, write them down. Eliminating sin at and coscats denire the ellipse write down equation of this ellipse, (m) Using what you have learnt in Lec 4, sketch the ellipse in parte) compute &, a and 'b' for this problem. Dont forget to show the direction of the phase projectory, on this m sketch. (B) we now add friction to our pendulum equation. The new equation is ** 2 x = x2 x = -12 sinx, -22. (h) Linearize 1 using Taylor's expansion in the vicinity of x= x=0, and , - write down M. X = MX stiw (i) Calculate the two complex eigenvalues of M. What are 6 and w for this problem. (j) Now calculate the complex eigenvector for the eigenvalue &tiw. (k) write down the solution vectors 3,(), , (+) Also write down the general solution X(t)= 4,8,0) + (2 8,10 For the initial condition X, (0:1, 2,0:1 calculates, and a + (1) Ignoring the pot { term as in Be define it, tits, write them down. Eliminating sin at and coscats denire the ellipse write down equation of this ellipse, (m) Using what you have learnt in Lec 4, sketch the ellipse in parte) compute &, a and 'b' for this problem. Dont forget to show the direction of the phase projectory, on this m sketch