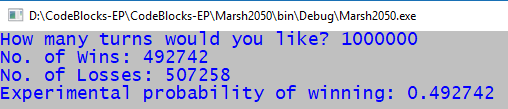
It can be shown analytically that the long term probability of winning the dice game you have programmed in PA 8-3 is .4929293. Extend that program you wrote to run a large number of turns and calculate the empirical (experimental) probability. 1,000,000 times through the for loop took about 2 seconds on a computer similar to those in the classroom. If yours takes longer than 10 seconds there is probably something wrong in your program. It is a good idea to run your loop only 100 or so times the first few times through. Hint: cast your # of wins and losses as float so you don't run into problems with integer division.

#include

#include

#include

using namespace std;

int main()

{

int sum;

int point;

int count;

int x,x2;

srand(time(0));

for (int i=1; i

{

x=rand()%6+1;

x2=rand()%6+1;

if (i ==1) {

point = x+x2;

cout

}

else if (point == 2 || point == 3|| point == 12 && i == i) {

cout

break;

}

else if (point == 7 || point ==11 && i == i) {

cout

break;

}

else {

cout

if (x+x2 == point && point !=7) {

cout

break;

}

if (x+x2 == 7 && i>0 && x+x2 != point) {

cout

break;

}

if (x+x2 != point && i == 7) {

cout

}

;}

}

}

//return 0;

DACodeBlocks-EP CodeBlocks-EP Marsh2050 bin\Debug\Marsh2050.exe How many turns would you like? 1000000 No. of Wins: 49274.2 No. of Losses: 507258 Experimental probability of winning: 0.492742