It is a Statistical Computation course assignment question, please see the question attached

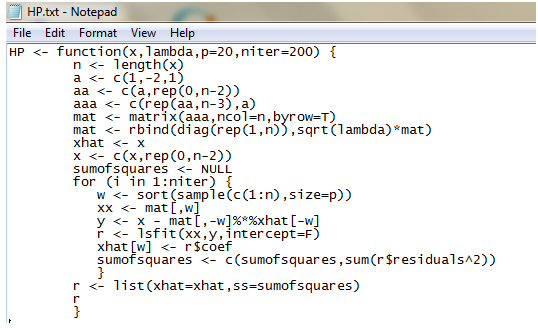
HP.txt - Notepad File Edit Format View Help HP 0 is a tuning parameter that controls the smoothness of the estimates 01, . . . , en- (This method is known as Whittaker graduation in actuarial science and the Hodrick- Prescott filter in economics.) (a) Show that if {yi} are exactly linear, i.e. y; = a x i + b for all i and some a and b then di = yi for all i. (b) In principal, we could compute 61, . ... en using ordinary least squares estimation. Show that 0 = (01, . .., 0,) minimizes lly - Xe|2 where y' is a vector of length 2n - 2 and X is an (2n -2) x n matrix. What are y" and X? (c) When n is large, computing 61, . .., , directly, for example, using the OLS formulation in part (b) is computationally expensive when n is large. Alternatively, we could use the Gauss-Seidel algorithm but it converges slowly, particularly for larger values of A. One possible alternatively is a randomized modification of the Gauss-Seidel algorithm, which at each stage solves a p( r