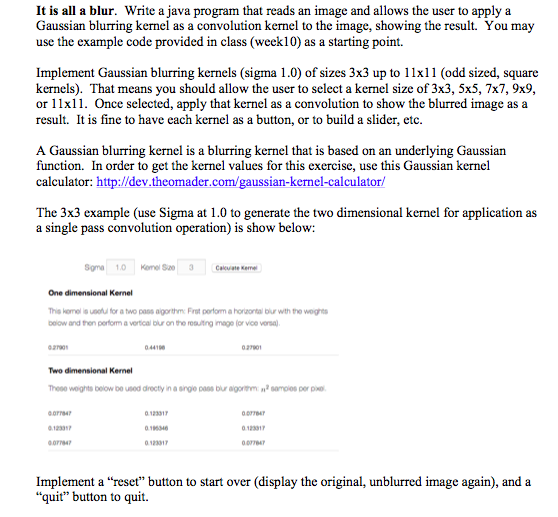
It is all a blur. Write a java program that reads an image and allows the user to apply a Gaussian blurring kernel as a convolution kernel to the image, showing the result. You may use the example code provided in class (weekl0) as a starting point. Implement Gaussian blurring kernels (sigma 1.0) of sizes 3x3 up to 11x (odd sized, square kernels). That means you should allow the user to select a kernel size of 3x3, 5x5, 7x7, 9x9 or 11xll. Once selected, apply that kernel as a convolution to show the blurred image as a result. It is fine to have each kernel as a button, or to build a slider, etc. 1 is a blurring k based on an underlying Gaussian A Gaussian blurring k function. In order to get the kernel values for this exercise, use this Gaussian kernel calculator: http://dev.theomader.com/gaussian-kernel-calculator/ The 3x3 example (use Sigma at 1.0 to generate the two dimensional kernel for application as a single pass convolution operation) is show below: One dimensional Kernel bolow and thon perfom a vertical bur on the rauting image for vice vorsa) Two dimensional Kernel 123317 1346 12331 1233 12331 0P784 03784 Implement a "reset" button to start over (display the original, unblurred image again), and a "quit" button to quit. It is all a blur. Write a java program that reads an image and allows the user to apply a Gaussian blurring kernel as a convolution kernel to the image, showing the result. You may use the example code provided in class (weekl0) as a starting point. Implement Gaussian blurring kernels (sigma 1.0) of sizes 3x3 up to 11x (odd sized, square kernels). That means you should allow the user to select a kernel size of 3x3, 5x5, 7x7, 9x9 or 11xll. Once selected, apply that kernel as a convolution to show the blurred image as a result. It is fine to have each kernel as a button, or to build a slider, etc. 1 is a blurring k based on an underlying Gaussian A Gaussian blurring k function. In order to get the kernel values for this exercise, use this Gaussian kernel calculator: http://dev.theomader.com/gaussian-kernel-calculator/ The 3x3 example (use Sigma at 1.0 to generate the two dimensional kernel for application as a single pass convolution operation) is show below: One dimensional Kernel bolow and thon perfom a vertical bur on the rauting image for vice vorsa) Two dimensional Kernel 123317 1346 12331 1233 12331 0P784 03784 Implement a "reset" button to start over (display the original, unblurred image again), and a "quit" button to quit