It is math 307 class and about the differential equation

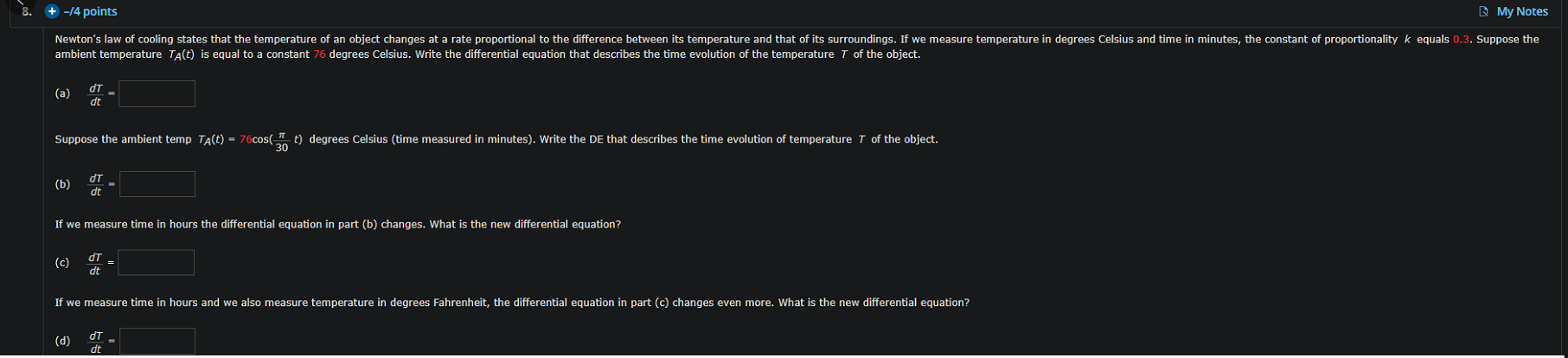
+-/4 points My Notes Newton's law of cooling states that the temperature of an object changes at a rate proportional to the difference between its temperature and that of its surroundings. If we measure temperature in degrees Celsius and time in minutes, the constant of proportionality k equals 0.3. Suppose the ambient temperature TA(t) is equal to a constant 76 degrees Celsius. Write the differential equation that describes the time evolution of the temperature 7 of the object. (a) Suppose the ambient temp TA(t) = 76cos( " ) degrees Celsius (time measured in minutes). Write the DE that describes the time evolution of temperature 7 of the object. (b) di dt If we measure time in hours the differential equation in part (b) changes. What is the new differential equation? (c) di = dt If we measure time in hours and we also measure temperature in degrees Fahrenheit, the differential equation in part (c) changes even more. What is the new differential equation? (d)