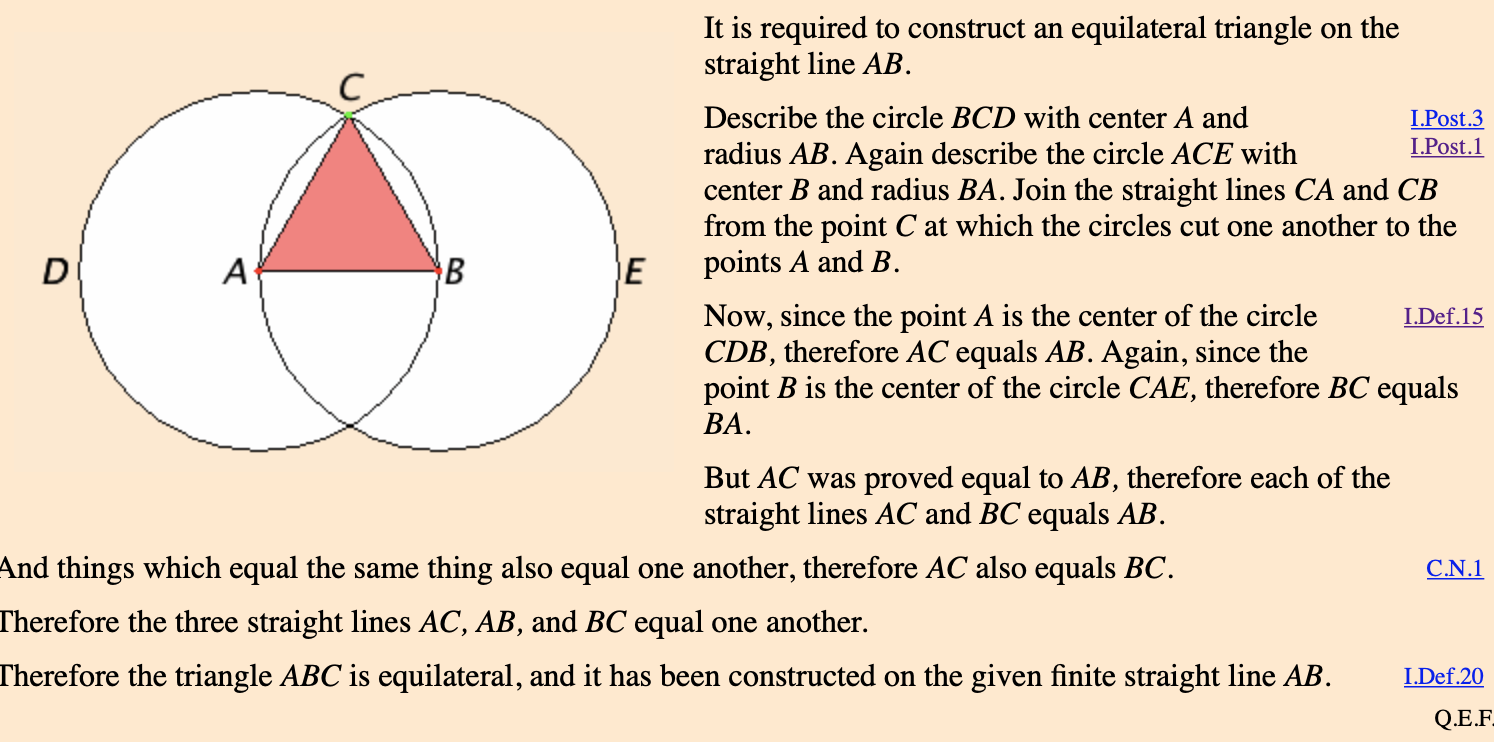
It is required to construct an equilateral triangle on the straight line AB. C Describe the circle BCD with center A and I.Post.3 radius AB. Again describe the circle ACE with I.Post.1 center B and radius BA. Join the straight lines CA and CB from the point C at which the circles cut one another to the D A E points A and B. Now, since the point A is the center of the circle I.Def.15 CDB, therefore AC equals AB. Again, since the point B is the center of the circle CAE, therefore BC equals BA. But AC was proved equal to AB, therefore each of the straight lines AC and BC equals AB. And things which equal the same thing also equal one another, therefore AC also equals BC. C.N.1 Therefore the three straight lines AC, AB, and BC equal one another. Therefore the triangle ABC is equilateral, and it has been constructed on the given finite straight line AB. I.Def.20 Q.E.FThe rational plane consists of all ordered pairs (any) of rational numbers (so '5, wt and so on are not allowed). All of Euclid's Postulates make sense in the rational plane. Review the proof of Book I, Proposition I. There is a step in the proof that does not make sense in the rational plane even though it does make sense in the usual real plane. Figure out what the step is and explain in a bit of detail what goes wrong. (Hint: try going through the proof starting with the line segment from (0,0) to (2,0) and see what happens.)