It's all the same to me

Please show logical proofs for each of the problems, citing which logical theorem/justification you are using at each step. Additionally, only the theorems/laws on the attached image should need to be used (with the addition of the Left Equivalence theorem described in problem part b. Thank you

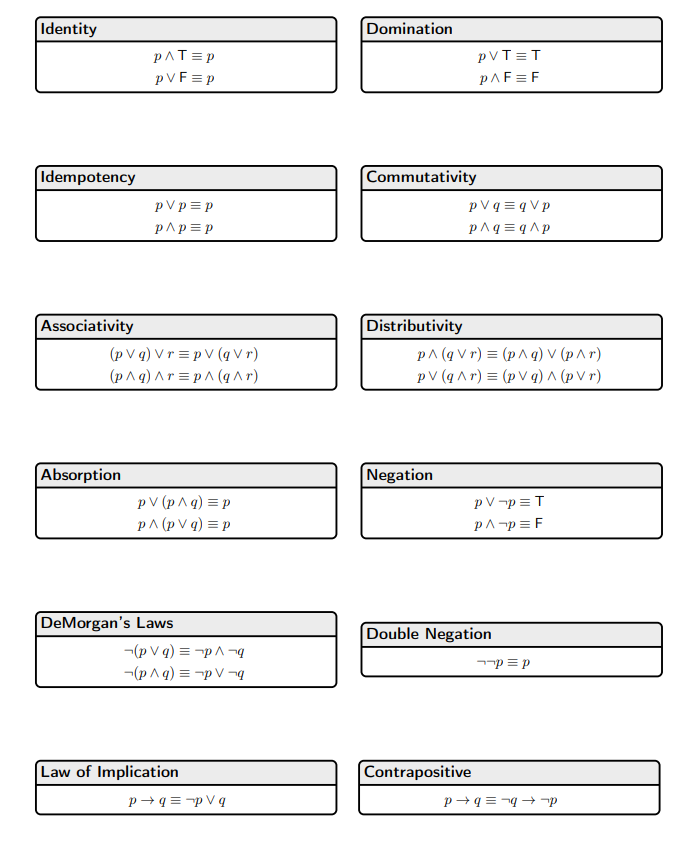
1. It's all the same to me... (18 points) Prove the following assertions using equivalences. You can use commutativity and associativity an arbitrary number of times in a single line of the proof. (a) [6 Points) p+(q + r) = ((p^q) + r). (b) [12 Points) (p+r)^(q + r) + (PV-) =T. (For this problem, for simplicity of presentation you can also use the "Left Distributive" laws, which say that (p Vq) Ar= (p Ar) V (Ar) and ( pq) Vr = (p Vr) A (Vr). These can be derived by using Commutativity once then ordinary Distributivity followed by two parallel applications of Commutativity.) Identity Domination PAT=p pVF=p PVT=T PAF=F Idempotency pvp =p pap=p Commutativity pVq=vp PAq=qip Associativity (pVg) Vr=pV (Vr) ( pq) Ar=pA (Ar) Distributivity pA (Vr) = ( pq) v (par) pv (Ar) = (pVg) (p Vr) Absorption Negation pv (19) =p pA (PV) =p pv-p=T PA-p=F Double Negation DeMorgan's Laws -(pVq) = 1 -( pq) = npV p=p Law of Implication p+q=pVq Contrapositive p+ = +=p